Tìm cực trị của các hàm số sau:
LG a
\(y = - 2{x^2} + 7x - 5\).
Phương pháp giải:
- Tính \( y'\).
- Tính \(y''\).
- Tính giá trị của \(y''\) tại các điểm làm cho \(y'=0\) và kết luận.
+ Các điểm làm cho \(y''<0\) thì đó là điểm cực đại.
+ Các điểm làm cho \(y''>0\) thì đó là điểm cực tiểu.
Lời giải chi tiết:
TXĐ: R
\(\eqalign{
& y' = - 4x + 7\cr &y' = 0 \Leftrightarrow - 4x + 7 = 0 \Leftrightarrow x = {7 \over 4} \cr
& y'' = - 4 \Rightarrow y''({7 \over 4}) = - 4 < 0 \cr} \)
Vậy \(x = {7 \over 4}\) là điểm cực đại của hàm số
\({y_{CD}} = - 2.{\left( {\frac{7}{4}} \right)^2} + 7.\frac{7}{4} - 5 = \frac{9}{8}\)
LG b
\(y = {x^3} - 3{x^2} - 24x + 7\)
Phương pháp giải:
- Tính \( y'\).
- Tính \(y''\).
- Tính giá trị của \(y''\) tại các điểm làm cho \(y'=0\) và kết luận.
+ Các điểm làm cho \(y''<0\) thì đó là điểm cực đại.
+ Các điểm làm cho \(y''>0\) thì đó là điểm cực tiểu.
Lời giải chi tiết:
TXĐ: R
\(y' = 3{x^2} - 6x - 24 = 3({x^2} - 2x - 8)\)
\(y' = 0 \Leftrightarrow {x^2} - 2x - 8 = 0\) \(\Leftrightarrow \left[ \matrix{
x = - 2 \hfill \cr
x = 4 \hfill \cr} \right.\)
\(y'' = 6x - 6\)
Vì \(y''( - 2) = 6.(-2)-6= - 18 < 0\) nên hàm số đạt cực đại tại \(x = - 2\) và yCĐ = y(-2) = 35.
\(y''(4) =6.4-6= 18 > 0\) nên hàm số đạt cực tiểu tại \( x = 4 \) và yCT = y(4) = -73.
LG c
\(y = {(x + 2)^2}{(x - 3)^3}\)
Phương pháp giải:
- Tính \( y'\).
- Lập bảng biến thiên và kết luận.
Lời giải chi tiết:
TXĐ: R
\(y' = 2(x + 2){(x - 3)^3} + 3{(x + 2)^2}{(x - 3)^2} \)
\(= \left( {x + 2} \right){\left( {x - 3} \right)^2}\left[ {2\left( {x - 3} \right) + 3\left( {x + 2} \right)} \right] \) \(= \left( {x + 2} \right){\left( {x - 3} \right)^2}\left( {2x - 6 + 3x + 6} \right)\)
\(= 5x(x + 2){(x - 3)^2}\)
\(y' = 0 \Leftrightarrow \left[ \matrix{
x = - 2 \hfill \cr
x = 0 \hfill \cr
x = 3 \hfill \cr} \right.\)
Bảng biến thiên:
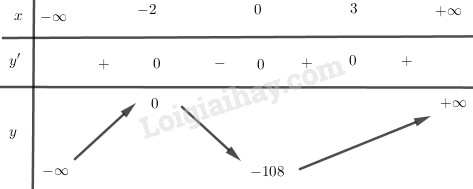
Từ đó suy ra yCĐ = y(-2) = 0 ; yCT = y(0) = -108.

