Tính thể tích của vật thể tròn xoay khi quay các hình phẳng giới hạn bởi các đường sau quanh trục Ox:
LG a
y = x3 ; y = 1 và x = 3
Lời giải chi tiết:
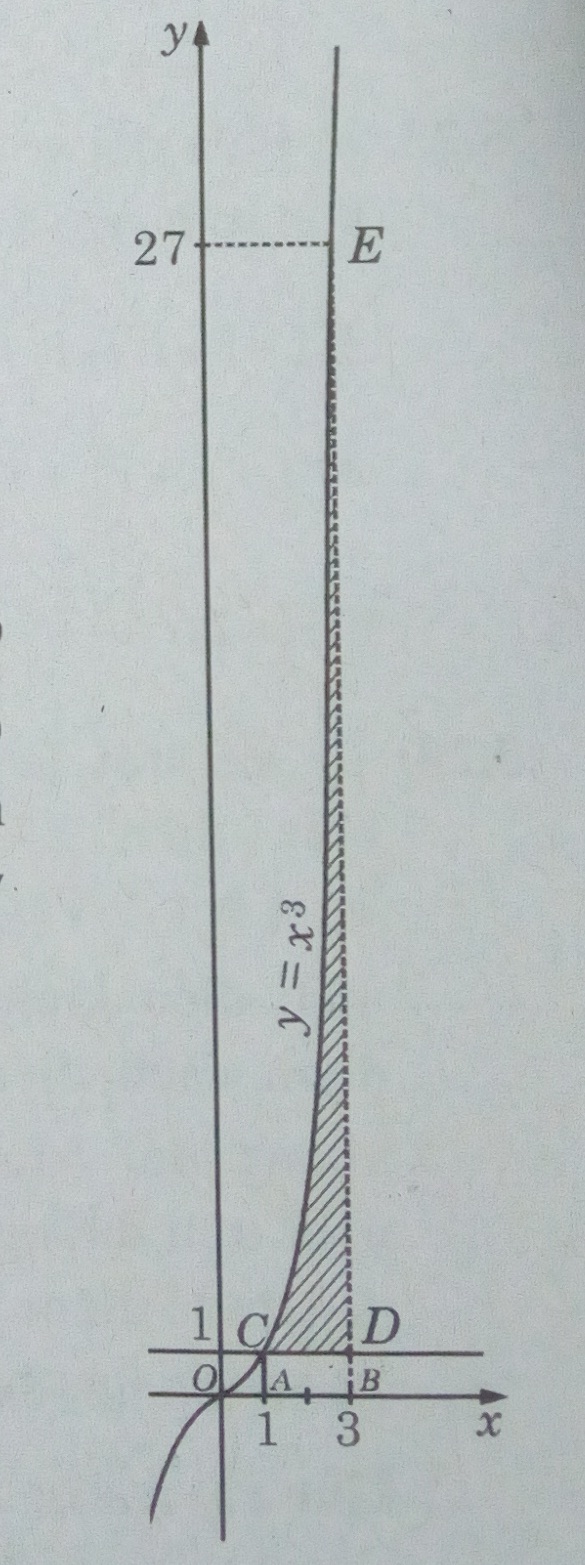
Thể tích vật thể tròn xoay sinh ra bởi miền CED quay quanh trục Ox là hiệu của hai thể tích (V1 và V2) của hai vật thể tròn xoay tương ứng sinh ra khi miền ACEB và miền ACDB quay quanh trục Ox. Như vậy V = V1 – V2 , trong đó :
\({V_1} = \pi \int\limits_1^3 {{x^6}} dx = {1 \over 7}\pi {x^7}\left| {\matrix{3 \cr 1 \cr} } \right. = {\pi \over 7}({3^7} - 1)\)
\({V_2} = \pi \int\limits_1^3 {dx = 2\pi }\)
\(\Rightarrow V = {V_1} - {V_2} = {\pi \over 7}({3^7} - 15) = 310{2 \over 7}\pi \) (đơn vị thể tích)
LG b
\(y = {2 \over \pi }x;y = \sin x;x \in {\rm{[}}0;{\pi \over 2}{\rm{]}}\)
Lời giải chi tiết:
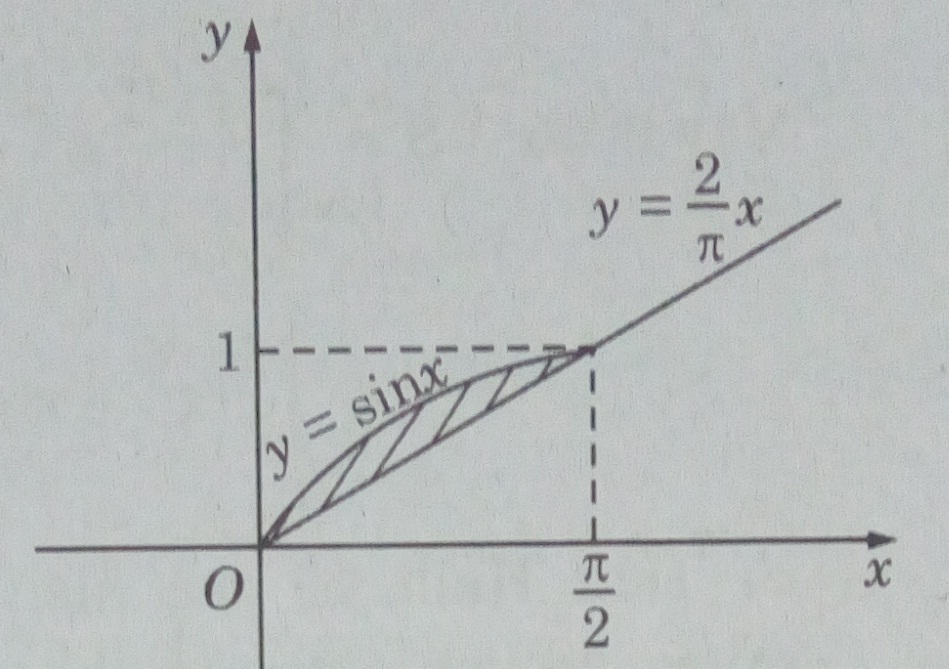
Ta có V = V1 – V2 trong đó
\({V_1} = \pi \int\limits_0^{{\pi \over 2}} {{{\sin }^2}xdx} \)
\(\begin{array}{l}
= \pi \int\limits_0^{\dfrac{\pi }{2}} {\dfrac{{1 - \cos 2x}}{2}dx} \\
= \dfrac{\pi }{2}\int\limits_0^{\dfrac{\pi }{2}} {\left( {1 - \cos 2x} \right)dx} \\
= \dfrac{\pi }{2}\left. {\left( {x - \dfrac{{\sin 2x}}{2}} \right)} \right|_0^{\dfrac{\pi }{2}}\\
= \dfrac{{{\pi ^2}}}{4}
\end{array}\)
\({V_2} = \pi \int\limits_0^{{\pi \over 2}} {{{({2 \over \pi }x)}^2}dx } \)
\( = \dfrac{4}{\pi }\int\limits_0^{\dfrac{\pi }{2}} {{x^2}dx} = \dfrac{4}{\pi }.\left. {\dfrac{{{x^3}}}{3}} \right|_0^{\dfrac{\pi }{2}} = \dfrac{{{\pi ^2}}}{6}\)
\(V = {V_1} - {V_2} = {{{\pi ^2}} \over {12}}\) (đơn vị thể tích)
LG c
\(y = {x^\alpha },\alpha \in {N^*};y = 0;x = 0\) và x = 1
Lời giải chi tiết:
Hình vẽ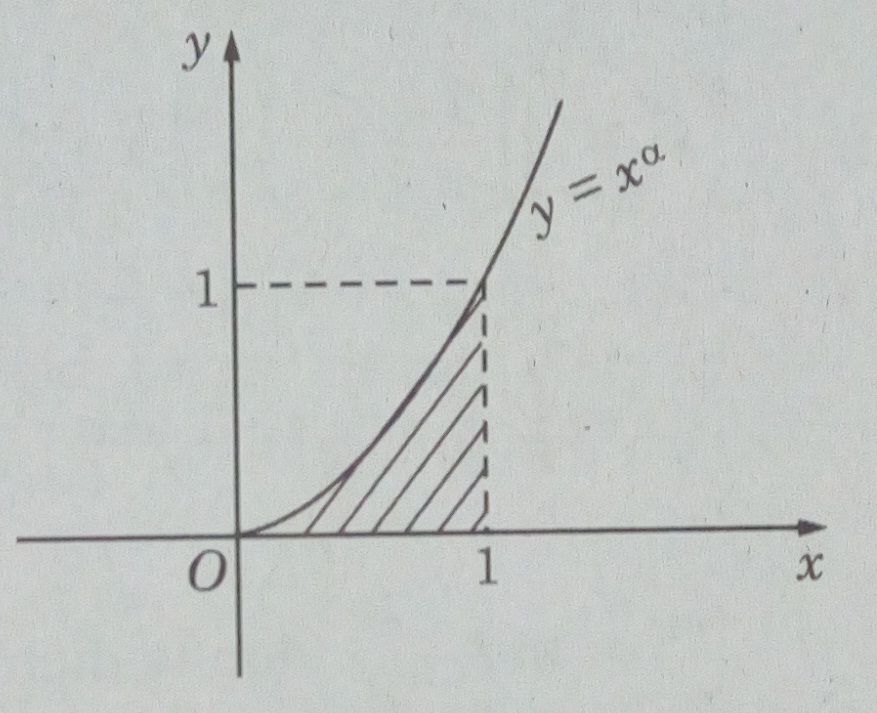
\(V = \pi \int\limits_0^1 {{x^{2\alpha }}dx} \)
\( = \pi .\left. {\dfrac{{{x^{2\alpha + 1}}}}{{2\alpha + 1}}} \right|_0^1 = \pi \left( {\dfrac{1}{{2\alpha + 1}} - 0} \right) \) \(= \dfrac{\pi }{{2\alpha + 1}}\)

