Đề bài
Tìm các giá trị của m để phương trình \({x^3}-3{x^2}-m = 0\) có ba nghiệm phân biệt.
Phương pháp giải - Xem chi tiết
- Biến đổi phương trình về dạng \(m = {x^3} - 3{x^2}\).
- Xét hàm \(f\left( x \right) = {x^3} - 3{x^2}\), lập bảng biến thiên và suy ra điều kiện \(m\) cần tìm.
Số nghiệm của phương trình bằng số giao điểm của đường thẳng với đồ thị hàm số.
Lời giải chi tiết
Ta có: \({x^3}-3{x^2}-m = 0\)\( \Leftrightarrow m = {x^3} - 3{x^2}\)
Xét hàm \(f\left( x \right) = {x^3} - 3{x^2}\) có \(f'(x) = 3{x^2} - 6x\)\( = 3x(x - 2) = 0 \Leftrightarrow \left[ {\begin{array}{*{20}{c}}{x = 0}\\{x = 2}\end{array}} \right.\).
Bảng biến thiên:
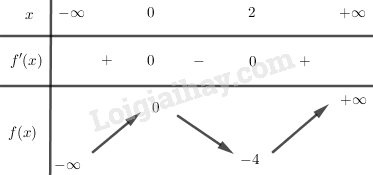
Phương trình \({x^3}-3{x^2}-m = 0\) có ba nghiệm phân biệt khi và chỉ khi đường thẳng \(y = m\) cắt đồ thị hàm số \(y = f\left( x \right)\) tại ba điểm phân biệt.
Từ bảng biến thiên suy ra \( - 4 < m < 0\) thỏa mãn bài toán.

