LG a
Khảo sát sự biến thiên và vẽ đồ thị (C) của hàm số: y=−x3+3x+1
Phương pháp giải:
- Tìm TXĐ.
- Xét sự biến thiên.
+ Tìm các giới hạn tại vô cực.
+ Tìm khoảng đồng biến, nghịch biến.
+ Tìm cực trị (nếu có).
+ Lập bảng biến thiên.
- Vẽ đồ thị hàm số.
Lời giải chi tiết:
* Tập xác định:D=R,
* Chiều biến thiên:
+) lim
+) y' = - 3{x^2} + 3; y' = 0 \Leftrightarrow \left[ {\begin{array}{*{20}{c}}{x = 1}\\{x = - 1}\end{array}} \right.
Hàm số nghịch biến trên mỗi khoảng ( - \infty ; - 1),(1; + \infty ).
Hàm số đồng biến trên khoảng \left( { - 1;1} \right).
Hàm số đạt cực đại tại x = 1,{y_{CD}} = 3. Hàm số đạt cực tiểu tại x = - 1,{y_{CT}} = - 1.
Bảng biến thiên:
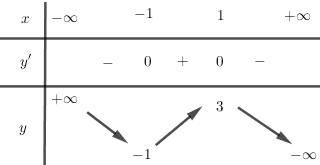
* Đồ thị:
+) Có y'' = - 6x; y'' = 0 \Leftrightarrow x = 0 \Rightarrow y = 1 nên điểm uốn U\left( {0;1} \right).
+) Đồ thị cắt trục Oy tại điểm \left( {0;1} \right).
+) Vẽ đồ thị:
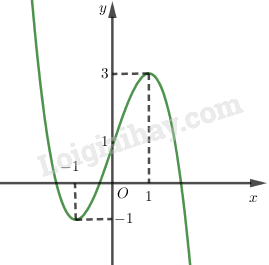
LG b
Chỉ ra phép biến hình biến \left( C \right) thành đồ thị \left( {C'} \right) của hàm số: y = {(x + 1)^3} - 3x - 4
Phương pháp giải:
Nhận xét dạng hàm số của \left( {C'} \right) so với \left( C \right), từ đó suy ra phép biến hình cần tìm.
Lời giải chi tiết:
Tịnh tiến \left( C \right) song song với trục Ox sang trái 1 đơn vị, ta được đồ thị \left( {{C_1}} \right) của hàm số y = f(x) = - {(x + 1)^3} + 3(x + 1) + 1 hay f(x) = - {(x + 1)^3} + 3x + 4 \left( {{C_1}} \right).
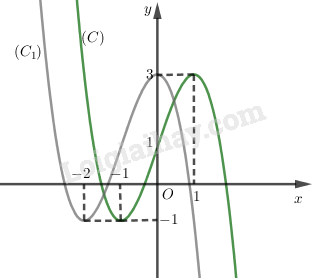
Lấy đối xứng \left( {{C_1}} \right) qua trục Ox, ta được đồ thị \left( {C'} \right) của hàm số y = g(x) = {(x + 1)^3} - 3x - 4
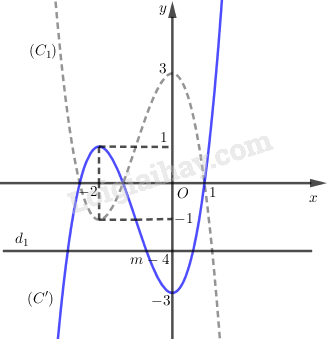
LG c
Dựa vào đồ thị \left( {C'} \right), biện luận theo m số nghiệm của phương trình: {(x + 1)^3} = 3x + m
Phương pháp giải:
- Biến đổi phương trình về dạng {(x + 1)^3} - 3x - 4 = m - 4.
- Từ đồ thị \left( {C'} \right) đã dựng và mối tương quan giữa số nghiệm của phương trình với tương giao đồ thị để biện luận.
Lời giải chi tiết:
Ta có: {(x + 1)^3} = 3x + m \Leftrightarrow {(x + 1)^3} - 3x - 4 = m - 4
Số nghiệm của phương trình đã cho là số giao điểm của hai đường y = g(x) = {(x + 1)^3} - 3x - 4 \left( {C'} \right)\; vày = m-4\left( {{d_1}} \right)
Từ đồ thị, ta suy ra:
+) Nếu \left[ \begin{array}{l}m - 4 < - 3\\m - 4 > 1\end{array} \right. \Leftrightarrow \left[ \begin{array}{l}m < 1\\m > 5\end{array} \right. thì phương trình đã cho có một nghiệm.
+) Nếu \left[ \begin{array}{l}m - 4 = - 3\\m - 4 = 1\end{array} \right. \Leftrightarrow \left[ \begin{array}{l}m = 1\\m = 5\end{array} \right. phương trình đã cho có hai nghiệm.
+) Nếu - 3 < m - 4 < 1 \Leftrightarrow 1 < m < 5, phương trình đã cho có ba nghiệm.
LG d
Viết phương trình tiếp tuyến \left( d \right) của đồ thị \left( {C'} \right), biết tiếp tuyến đó vuông góc với đường thẳng y = - \dfrac{x}{9} + 1
Phương pháp giải:
- Tìm hệ số góc k của d, sử dụng tính chất hai đường thẳng vuông góc nếu tích hai hệ số góc bằng - 1.
- Giải phương trình y' = k tìm hoành độ tiếp điểm, suy ra tung độ.
- Viết phương trình tiếp tuyến tho công thức y = k\left( {x - {x_0}} \right) + {y_0}.
Lời giải chi tiết:
Vì \left( d \right) vuông góc với đường thẳng y = - \dfrac{x}{9} + 1 nên ta có hệ số góc bằng 9.
Ta có: g'(x) = 3{(x + 1)^2} - 3
g'(x) = 9 \Leftrightarrow 3{\left( {x + 1} \right)^2} - 3 = 9 \Leftrightarrow {\left( {x + 1} \right)^2} = 4 \Leftrightarrow \left[ \begin{array}{l}x + 1 = 2\\x + 1 = - 2\end{array} \right. \Leftrightarrow \left[ \begin{array}{l}x = 1 \Rightarrow y = 1\\x = - 3 \Rightarrow y = - 3\end{array} \right.
+ Với x = 1,y = 1 ta có tiếp tuyến: y = 9\left( {x - 1} \right) + 1 hay y = 9x - 8.
+ Với x = - 3,y = - 3 ta có tiếp tuyến: y = 9\left( {x + 3} \right) - 3 hay y = 9x + 24.
Vậy có hai tiếp tuyến phải tìm là: y = 9x - 8 và y = 9x + 24.
