Đề bài
Cho ba đoạn thẳng bằng nhau, đôi một vuông góc với nhau và cắt nhau tại trung điểm của chúng. Chứng minh rằng các đầu mút của ba đoạn thẳng ấy là các đỉnh của một hình bát diện đều.
Phương pháp giải - Xem chi tiết
Sử dụng lý thuyết về định nghĩa khối bát diện đều để chứng minh:
Khối bát diện đều là khối đa diện lồi có các mặt là các tam giác đều, mỗi đỉnh là đỉnh chung của \(4\) cạnh.
Lời giải chi tiết
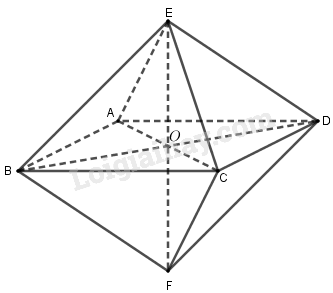
Ta chứng minh tám mặt của khối bát diện trên là các tam giác đều.
Gọi ba đoạn thẳng \(AC,BD,EF\) có độ dài bằng \(a\) cắt nhau tại trung điểm \(O\) của mỗi đường.
Khi đó \(OA = OB = OC\) \( = OD = OE = OF = \dfrac{a}{2}\).
Tam giác \(EOC\) vuông cân tại \(O\) có \(OE = OC = \dfrac{a}{2}\) nên \(EC = \dfrac{{a\sqrt 2 }}{2}\).
Tương tự cũng tính được \(EA = EB = ED = FA\) \( = FB = FC = FD = \dfrac{{a\sqrt 2 }}{2}\).
Vậy \(ABCDEF\) là hình bát diện đều.

