Khảo sát và vẽ đồ thị các hàm số:
LG a
a) \(y = \dfrac{{x - 2}}{{x + 1}}\)
Phương pháp giải:
* Tìm TXĐ.
* Xét sự biến thiên:
+ Tính \(y'\).
+ Tìm khoảng đồng biến, nghịch biến.
+ Tìm các đường tiệm cận.
+ Lập bảng biến thiên.
* Vẽ đồ thị hàm số.
Giải chi tiết:
* TXĐ: \(D = \mathbb{R}\backslash \left\{ { - 1} \right\}\).
* Chiều biến thiên: \(y' = \dfrac{3}{{{{\left( {x + 1} \right)}^2}}} > 0,\forall x \ne - 1\)
Do đó hàm số đồng biến trên các khoảng \(\left( { - \infty ; - 1} \right)\) và \(\left( { - 1; + \infty } \right)\).
Có \(\mathop {\lim }\limits_{x \to \pm \infty } y = 1\) nên TCN \(y = 1\) và \(\mathop {\lim }\limits_{x \to - {1^ + }} y = - \infty ,\mathop {\lim }\limits_{x \to - {1^ - }} y = + \infty \) nên TCĐ: \(x = - 1\).
Bảng biến thiên:
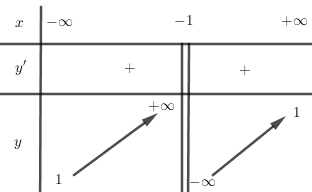
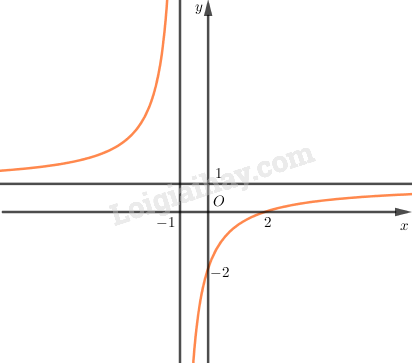
* Đồ thị:
- Cắt trục \(Oy\) tại điểm \(\left( {0; - 2} \right)\) và cắt trục \(Ox\) tại điểm \(\left( {2;0} \right)\).
- Nhận giao điểm hai đường tiệm cận \(I\left( { - 1;1} \right)\) làm tâm đối xứng.
LG b
\(y = \dfrac{{2 - x}}{{2x - 1}} = \dfrac{{ - x + 2}}{{2x - 1}}\)
Phương pháp giải:
* Tìm TXĐ.
* Xét sự biến thiên:
+ Tính \(y'\).
+ Tìm khoảng đồng biến, nghịch biến.
+ Tìm các đường tiệm cận.
+ Lập bảng biến thiên.
* Vẽ đồ thị hàm số.
Giải chi tiết:
* TXĐ: \(D = \mathbb{R}\backslash \left\{ {\dfrac{1}{2}} \right\}\).
* Chiều biến thiên: \(y' = \dfrac{{ - 3}}{{{{\left( {2x - 1} \right)}^2}}} < 0,\forall x \ne \dfrac{1}{2}\)
Do đó hàm số nghịch biến trên các khoảng \(\left( { - \infty ;\dfrac{1}{2}} \right)\) và \(\left( {\dfrac{1}{2}; + \infty } \right)\).
Có \(\mathop {\lim }\limits_{x \to \pm \infty } y = - \dfrac{1}{2}\) nên TCN \(y = - \dfrac{1}{2}\) và \(\mathop {\lim }\limits_{x \to {{\left( {\dfrac{1}{2}} \right)}^ + }} y = + \infty ,\mathop {\lim }\limits_{x \to {{\left( {\dfrac{1}{2}} \right)}^ - }} y = - \infty \) nên TCĐ: \(x = \dfrac{1}{2}\).
Bảng biến thiên:
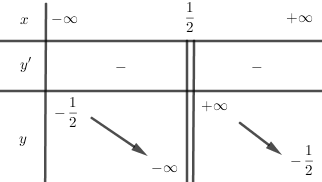
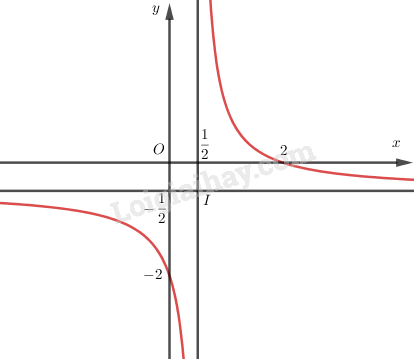
* Đồ thị:
- Cắt trục \(Oy\) tại điểm \(\left( {0; - 2} \right)\) và cắt trục \(Ox\) tại điểm \(\left( {2;0} \right)\).
- Nhận giao điểm hai đường tiệm cận \(I\left( {\dfrac{1}{2}; - \dfrac{1}{2}} \right)\) làm tâm đối xứng.
- Vẽ đồ thị: