Tìm giá trị lớn nhất, giá trị nhỏ nhất của các hàm số sau:
LG a
\(f(x) = \sqrt {25 - {x^2}} \) trên đoạn \(\left[ { - 4;4} \right]\)
Phương pháp giải:
- Tính \(f'\left( x \right)\), tìm các điểm trong đoạn \(\left[ {a;b} \right]\) làm cho \(f'\left( x \right) = 0\) và không xác định.
- Tính giá trị của hàm số tại các điểm trên, so sánh và kết luận.
Giải chi tiết:
Ta có: \(f'(x) = \dfrac{{ - x}}{{\sqrt {25 - {x^2}} }} = 0\) \( \Leftrightarrow x = 0 \in \left[ { - 4;4} \right]\)
Mặt khác, ta có \(f\left( { - 4} \right) = f\left( 4 \right) = 3\); \(f\left( 0 \right) = 5\).
Vậy \(\mathop {\min }\limits_{{\rm{[}} - 4;4]} f(x) = 3;\mathop {\max }\limits_{{\rm{[}} - 4;4]} f(x) = 5\)
LG b
\(f(x) = |{x^2} - 3x + 2|\) trên đoạn \(\left[ { - 10;10} \right]\)
Phương pháp giải:
- Lập bảng biến thiên của hàm số \(y = g\left( x \right) = {x^2}-3x + 2\).
- Từ đó suy ra bảng biến thiên của hàm số \(y = f\left( x \right) = \left| {g\left( x \right)} \right|\).
Giải chi tiết:
Khảo sát sự biến thiên và vẽ đồ thị của hàm số \(y = g\left( x \right) = {x^2}-3x + 2\).
Ta có: \(g'(x) = 2x - 3;g'(x) = 0 \Leftrightarrow x = \dfrac{3}{2}\)
Bảng biến thiên:
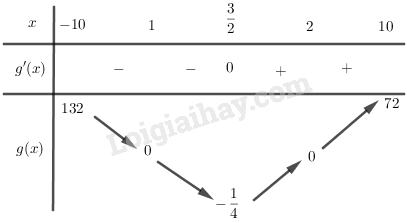
Vì \(f(x) = \left\{ {\begin{array}{*{20}{c}}{g(x),{x^2} - 3x + 2 \ge 0}\\{ - g(x),{x^2} - 3x + 2 < 0}\end{array}} \right.\) nên ta có bảng biến thiên của \(y = f\left( x \right) = \left| {g\left( x \right)} \right|\) như sau:
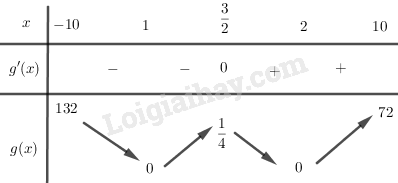
Từ bảng biên thiên suy ra: \(\mathop {\min }\limits_{{\rm{[}} - 10;10]} f(x) = f(1) = f(2) = 0;\)\(\mathop {\max }\limits_{{\rm{[}} - 10;10]} f(x) = f( - 10) = 132\)
LG c
\(f(x) = \dfrac{1}{{\sin x}}\) trên đoạn \(\left[ {\dfrac{\pi }{3};\dfrac{{5\pi }}{6}} \right]\)
Phương pháp giải:
- Tính \(f'\left( x \right)\), tìm các điểm trong đoạn \(\left[ {a;b} \right]\) làm cho \(f'\left( x \right) = 0\) và không xác định.
- Tính giá trị của hàm số tại các điểm trên, so sánh và kết luận.
Giải chi tiết:
Ta có: \(f'\left( x \right) = - \dfrac{{\cos x}}{{{{\sin }^2}x}} = 0\) \( \Leftrightarrow x = \dfrac{\pi }{2} + k\pi ,k \in \mathbb{Z}\).
Mà \(x \in \left[ {\dfrac{\pi }{3};\dfrac{{5\pi }}{6}} \right]\)nên \(x = \dfrac{\pi }{2}\).
Mà \(f\left( {\dfrac{\pi }{3}} \right) = \dfrac{2}{{\sqrt 3 }},f\left( {\dfrac{{5\pi }}{6}} \right) = 2\), \(f\left( {\dfrac{\pi }{2}} \right) = 1\).
Vậy \(\mathop {\min }\limits_{\left[ {\dfrac{\pi }{3};\dfrac{{5\pi }}{6}} \right]} f(x) = 1;\mathop {\max }\limits_{\left[ {\dfrac{\pi }{3};\dfrac{{5\pi }}{6}} \right]} f(x) = 2\).
LG d
\(f(x) = 2\sin x + \sin 2x\) trên đoạn \(\left[ {0;\dfrac{{3\pi }}{2}} \right]\)
Phương pháp giải:
- Tính \(f'\left( x \right)\), tìm các điểm trong đoạn \(\left[ {a;b} \right]\) làm cho \(f'\left( x \right) = 0\) và không xác định.
- Tính giá trị của hàm số tại các điểm trên, so sánh và kết luận.
Giải chi tiết:
Ta có: \(f'(x) = 2\cos x + 2\cos 2x\)\( = 4\cos \dfrac{x}{2}\cos \dfrac{{3x}}{2}\)
\(f'(x) = 0\)\( \Leftrightarrow \left[ {\begin{array}{*{20}{c}}{\cos \dfrac{x}{2} = 0}\\{\cos \dfrac{{3x}}{2} = 0}\end{array}} \right. \Rightarrow \left[ {\begin{array}{*{20}{c}}{x = \pi }\\{x = \dfrac{\pi }{3}}\end{array}} \right.\) (do \(x \in \left[ {0;\dfrac{{3\pi }}{2}} \right]\))
Ta có: \(f(0) = 0,f\left( {\dfrac{\pi }{3}} \right) = \dfrac{{3\sqrt 3 }}{2},\)\(f(\pi ) = 0,f\left( {\dfrac{{3\pi }}{2}} \right) = - 2\)
Vậy \(\mathop {\min }\limits_{\left[ {0;\dfrac{{3\pi }}{2}} \right]} f(x) = - 2;\)\(\mathop {\max }\limits_{\left[ {0;\dfrac{{3\pi }}{2}} \right]} f(x) = \dfrac{{3\sqrt 3 }}{2}\).

