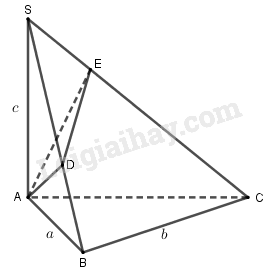
Cho hình chóp tam giác \(S.ABC\) có đáy là tam giác vuông ở \(B\). Cạnh \(SA\) vuông góc với đáy. Từ \(A\) kẻ các đoạn thẳng \(AD\) vuông góc với \(SB\) và \(AE\) vuông góc với \(SC\). Biết rằng \(AB = a,BC = b,SA = c\).
LG a
Hãy tính thể tích khối chóp \(S.ADE\)
Phương pháp giải:
- Chứng minh \(SE \bot \left( {ADE} \right)\).
- Tính diện tích tam giác \(ADE\) và chiều cao \(SE\).
- Tính thể tích khối chóp theo công thức \(V = \dfrac{1}{3}Sh\).
Giải chi tiết:
Ta có \(\left\{ {\begin{array}{*{20}{c}}{BC \bot SA}\\{BC \bot AB}\end{array}} \right. \Rightarrow BC \bot (SAB)\)
Vì \(AD \subset (SAB)\) nên \(AD \bot BC\)
Mặt khác \(AD \bot SB\) nên \(AD \bot (SBC)\)
Từ đó suy ra \(AD \bot SC\)
\(\left\{ {\begin{array}{*{20}{c}}{SC \bot AE}\\{SC \bot AD}\end{array}} \right.\)\( \Rightarrow SC \bot (ADE) \Rightarrow SC \bot DE\) hay \(SE \bot (ADE)\).
Trong tam giác vuông \(SAB\) ta có: \(SA.AB = AD.SB\)\( \Rightarrow AD = \dfrac{{AB.SA}}{{SB}} = \dfrac{{ac}}{{\sqrt {{a^2} + {c^2}} }}\)
Tương tự, trong tam giác vuông \(SAC\) ta có: \(AE = \dfrac{{SA.AC}}{{SC}} = \dfrac{{c\sqrt {{a^2} + {b^2}} }}{{\sqrt {{a^2} + {b^2} + {c^2}} }}\)
Do \(AD \bot (SBC)\) nên \(AD \bot DE\). Từ đó suy ra:
\(DE = \sqrt {A{E^2} - A{D^2}} \)\( = \sqrt {\dfrac{{{c^2}({a^2} + {b^2})}}{{{a^2} + {b^2} + {c^2}}} - \dfrac{{{a^2}{c^2}}}{{{a^2} + {c^2}}}} \) \( = \dfrac{{{c^2}b}}{{\sqrt {({a^2} + {b^2} + {c^2})({a^2} + {c^2})} }}\)
\(SE = \sqrt {S{A^2} - A{E^2}} \)\( = \sqrt {{c^2} - \dfrac{{{c^2}({a^2} + {b^2})}}{{{a^2} + {b^2} + {c^2}}}} \) \( = \dfrac{{{c^2}}}{{\sqrt {{a^2} + {b^2} + {c^2}} }}\)
Vậy \({V_{S.ADE}} = \dfrac{1}{3}.\dfrac{1}{2}AD.DE.SE\)\( = \dfrac{1}{6}\dfrac{{ac}}{{\sqrt {{a^2} + {c^2}} }}.\dfrac{{{c^2}b}}{{\sqrt {({a^2} + {b^2} + {c^2})({a^2} + {c^2})} }}.\dfrac{{{c^2}}}{{\sqrt {{a^2} + {b^2} + {c^2}} }}\)
\( = \dfrac{{ab{c^5}}}{{6({a^2} + {b^2} + {c^2})({a^2} + {c^2})}}\)
LG b
Tính khoảng cách từ \(E\) đến mặt phẳng \(\left( {SAB} \right)\).
Phương pháp giải:
- Tính diện tích tam giác \(SAD\).
- Sử dụng công thức \({V_{SADE}} = \dfrac{1}{3}d.{S_{SAD}}\) và kết quả câu a để suy ra \(d\).
Giải chi tiết:
Gọi \(d\) là khoảng cách từ \(E\;\) đến mặt phẳng \(\left( {SAB} \right)\)
Ta có: \(SD = \sqrt {S{A^2} - A{D^2}} \)\( = \sqrt {{c^2} - \dfrac{{{a^2}{c^2}}}{{{a^2} + {c^2}}}} = \dfrac{{{c^2}}}{{\sqrt {{a^2} + {c^2}} }}\)
\({V_{S.ADE}} = {V_{E.SAD}}\)\( = \dfrac{1}{3}.\dfrac{1}{2}SD.AD.d\) \( = \dfrac{1}{6}.\dfrac{{{c^2}}}{{\sqrt {{a^2} + {c^2}} }}.\dfrac{{ac}}{{\sqrt {{a^2} + {c^2}} }}.d\) \( = \dfrac{1}{6}.\dfrac{{a{c^3}}}{{{a^2} + {c^2}}}.d\)
Kết hợp với kết quả trong câu a ta suy ra \(d = \dfrac{{b{c^2}}}{{{a^2} + {b^2} + {c^2}}}\).

