Đề bài
Cho hình chóp tứ giác đều \(S.ABCD\) có mặt bên tạo với đáy một góc bằng \({60^0}\) và diện tích một mặt bên bằng \(\dfrac{{{a^2}}}{2}\). Thể tích của hình chóp bằng:
A. \(\dfrac{{\sqrt 3 }}{9}{a^3}\) B. \(\dfrac{{\sqrt 3 }}{6}{a^3}\)
C. \(\dfrac{{\sqrt 3 }}{3}{a^3}\) D. \(\dfrac{{\sqrt 3 }}{2}{a^3}\)
Phương pháp giải - Xem chi tiết
- Xác định góc tạo bởi mặt bên và mặt đáy của hình chóp.
- Tính diện tích đáy và chiều cao của hình chóp và suy ra thể tích.
Lời giải chi tiết
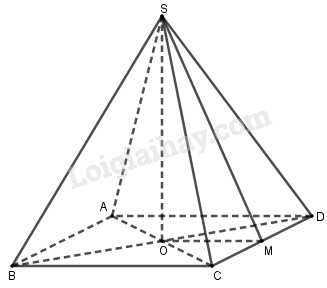
Gọi \(M\) là trung điểm của \(CD\), \(O\) là tâm của hình vuông \(ABCD\).
Đặt \(CD = x\). Do \({S_{SCD}} = \dfrac{{{a^2}}}{2}\) \( \Rightarrow SM = \dfrac{{2{S_{SCD}}}}{{CD}} = \dfrac{{{a^2}}}{x}\)
Lại có \(OM \bot CD,SM \bot CD\) nên góc giữa \(\left( {SCD} \right)\) và \(\left( {ABCD} \right)\) bằng \(\widehat {SMO} = {60^0}\)
Tam giác \(SOM\) vuông tại \(O\) có \(OM = \dfrac{x}{2}\), \(SM = \dfrac{{{a^2}}}{x}\) và \(\widehat {SMO} = {60^0}\)
\( \Rightarrow \cos {60^0} = \dfrac{{OM}}{{SM}}\) \( \Leftrightarrow \dfrac{1}{2} = \dfrac{x}{2}:\dfrac{{{a^2}}}{x} \Leftrightarrow x = a\)
\( \Rightarrow OM = \dfrac{a}{2},SM = a\) \( \Rightarrow SO = \sqrt {S{M^2} - O{M^2}} = \dfrac{{a\sqrt 3 }}{2}\)
Vậy thể tích \({V_{S.ABCD}} = \dfrac{1}{3}{S_{ABCD}}.SO\) \( = \dfrac{1}{3}.{a^2}.\dfrac{{a\sqrt 3 }}{2} = \dfrac{{{a^3}\sqrt 3 }}{6}\).
Chọn B.

