LG a
Khảo sát sự biến thiên và vẽ đồ thị \(\left( C \right)\) của hàm số \(y = \dfrac{{x + 2}}{{x - 3}}\)
Phương pháp giải:
- Tìm TXĐ.
- Xét sự biến thiên.
- Vẽ đồ thị hàm số.
Giải chi tiết:
TXĐ: \(D = \mathbb{R}\backslash \left\{ 3 \right\}\).
Có \(y' = \dfrac{{ - 5}}{{{{\left( {x - 3} \right)}^2}}} < 0,\forall x \ne 3\) nên hàm số luôn nghịch biến trên các khoảng \(\left( { - \infty ;3} \right)\) và \(\left( {3; + \infty } \right)\).
Hàm số đã cho không có cực trị.
TCĐ: \(x = 3\) và TCN \(y = 1\).
Bảng biến thiên:
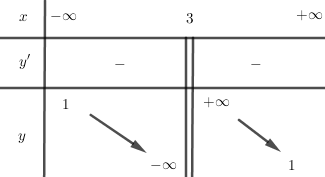
Đồ thị:
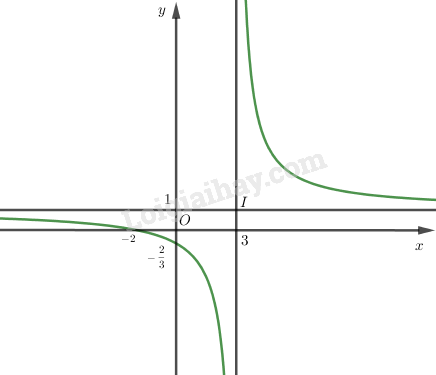
LG b
Chứng minh rằng giao điểm \(I\) của hai tiệm cận của \(\left( C \right)\) là tâm đối xứng của \(\left( C \right)\).
Phương pháp giải:
- Tìm tọa độ giao điểm hai đường tiệm cận.
- Viết công thức đổi tọa độ suy ra phương trình của hàm số trong hệ tọa độ mới.
Công thức tịnh tiến hệ tọa độ:
Cho điểm \(I\left( {{x_0};{y_0}} \right),M\left( {x;y} \right)\) đối với hệ tọa độ \(Oxy\).
Công thức chuyển hệ tọa độ trong phép tịnh tiến theo véc tơ \(\overrightarrow {OI} \) là: \(\left\{ \begin{array}{l}x = X + {x_0}\\y = Y + {y_0}\end{array} \right.\)
Khi đó điểm \(I\left( {0;0} \right),M\left( {X,Y} \right)\) đối với hệ tọa độ \(IXY\).
- Kiểm tra hàm số trong hệ tọa độ mới có làm hàm số lẻ hay không và kết luận.
Nếu hàm số \(Y = g\left( X \right)\) là hàm số lẻ (trong hệ tọa độ mới \(IXY\)) thì điểm \(I\left( {{x_0};{y_0}} \right)\) trong hệ tọa độ \(Oxy\) là tâm đối xứng của đồ thị hàm số \(y = f\left( x \right)\).
Giải chi tiết:
Tiệm cận đứng là đường thẳng \(x = 3\).
Tiệm cận ngang là đường thẳng \(y = 1\).
Do đó, giao điểm của hai đường tiệm cận là \(I\left( {3;1} \right)\).
Thực hiện phép biến đổi: \(\left\{ {\begin{array}{*{20}{c}}{x = X + 3}\\{y = Y + 1}\end{array}} \right.\) ta được \(Y + 1 = \dfrac{{X + 5}}{X}\)\( \Leftrightarrow Y = \dfrac{{X + 5}}{X} - 1 \Leftrightarrow Y = \dfrac{5}{X}\).
Vì \(Y = \dfrac{5}{X}\) là hàm số lẻ nên đồ thị \(\left( C \right)\) của hàm số này có tâm đối xứng là gốc tọa độ \(I\) của hệ tọa độ \(IXY\).
Vậy đồ thị hàm số đã cho nhận điểm \(I\left( {3;1} \right)\) làm tâm đối xứng trong hệ tọa độ cũ.
LG c
Tìm điểm \(M\) trên đồ thị của hàm số sao cho khoảng cách từ \(M\) đến tiệm cận đứng bằng khoảng cách từ \(M\) đến tiệm cận ngang.
Phương pháp giải:
- Gọi điểm \(M({x_0};{y_0}) \in (C)\).
- Tính khoảng cách từ \(M\) đến các đường tiệm cận.
- Lập phương trình ẩn \({x_0}\), dựa vào điều kiện khoảng cách bằng nhau của đề bài.
- Giải phương trình tìm \({x_0}\) và kết luận.
Giải chi tiết:
Giả sử \(M({x_0};{y_0}) \in (C)\).
Gọi \({d_1}\) là khoảng cách từ \(M\) đến tiệm cận đứng và \({d_2}\) là khoảng cách từ \(M\) đến tiệm cận ngang, ta có: \({d_1} = \left| {{x_0} - 3} \right|,\)\({d_2} = \left| {{y_0} - 1} \right| = \dfrac{5}{{|{x_0} - 3|}}\)
Suy ra \(\left| {{x_0} - 3} \right| = \dfrac{5}{{\left| {{x_0} - 3} \right|}}\) \( \Leftrightarrow {\left( {{x_0} - 3} \right)^2} = 5\) \( \Leftrightarrow \left[ \begin{array}{l}{x_0} - 3 = \sqrt 5 \\{x_0} - 3 = - \sqrt 5 \end{array} \right.\) \( \Leftrightarrow \left[ \begin{array}{l}{x_0} = 3 + \sqrt 5 \\{x_0} = 3 - \sqrt 5 \end{array} \right.\)
Với \({x_0} = 3 + \sqrt 5 \Rightarrow {y_0} = 1 + \sqrt 5 \) nên ta có điểm \(M\left( {3 + \sqrt 5 ;1 + \sqrt 5 } \right)\).
Với \({x_0} = 3 - \sqrt 5 \Rightarrow {y_0} = 1 - \sqrt 5 \) nên ta có điểm \(M\left( {3 - \sqrt 5 ;1 - \sqrt 5 } \right)\).
Vậy có hai điểm \({M_1}\left( {3 + \sqrt 5 ;1 + \sqrt 5 } \right)\) và \({M_2}\left( {3 - \sqrt 5 ;1 - \sqrt 5 } \right)\).

