Đề bài
Cho hình hộp \(ABCD.A'B'C'D'\). Gọi \(E\) và \(F\) lần lượt là trung điểm của \(B'C'\) và \(C'D'\). Mặt phẳng \(\left( {AEF} \right)\) chia hình hộp đó thành hai hình đa diện \(\left( H \right)\) và \(\left( {H'} \right)\), trong đó \(\left( H \right)\) là hình đa diện chứa đỉnh \(A'\). Tính tỉ số giữa thể tích hình đa diện \(\left( H \right)\) và thể tích hình đa diện \(\left( {H'} \right)\).
Phương pháp giải - Xem chi tiết
- Xác định thiết diện của hình hộp khi cắt bởi \(\left( {AEF} \right)\).
- Đặt thể tích khối hộp \(ABCD.A'B'C'D'\) là \(V\).
- Tính thể tích khối đa diện \(\left( H \right)\) bằng phương pháp phân chia khối đa diện.
Chú ý: Công thức tỉ số thể tích của hai khối chóp tam giác \(S.A'B'C'\) và \(S.ABC\) với \(A' \in SA,B' \in SB,C' \in SC\) là \(\dfrac{{{V_{S.A'B'C'}}}}{{{V_{S.ABC}}}} = \dfrac{{SA'}}{{SA}}.\dfrac{{SB'}}{{SB}}.\dfrac{{SC'}}{{SC}}\).
Lời giải chi tiết
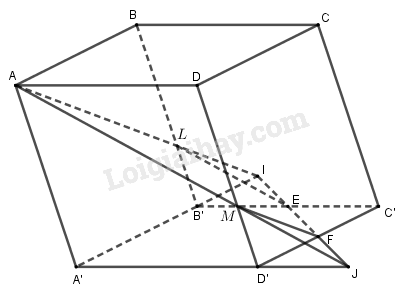
Trong \(\left( {A'B'C'D'} \right)\), gọi \(I,J\) lần lượt là giao điểm của \(EF\) với \(A'B'\) và \(A'D'\).
Trong \(\left( {ADD'A'} \right)\), gọi \(M = AJ \cap D'D\).
Trong \(\left( {ABB'A'} \right)\), gọi \(L = AI \cap BB'\).
Khi đó thiết diện của hình hộp khi cắt bởi \(\left( {AEF} \right)\) là ngũ giác \(AMFEL\).
Khi đó \(\left( H \right)\) là khối đa diện chứ đỉnh \(A'\) và \({V_{\left( H \right)}} = {V_{A.A'IJ}} - {V_{M.D'JF}} - {V_{L.B'IE}}\).
Gọi \({V_0}\) là thể tích khối tứ diện\(A.A'IJ\). \(V\) là thể tích khối hộp \(ABCD.A'B'C'D'\).
Vì \(EB' = EC'\) và \(B'I//C'F\) nên \(IB' = FC' = \dfrac{{A'B'}}{2}\)
Do đó \(\dfrac{{IB'}}{{IA'}} = \dfrac{1}{3}\)
Mà \(BE'//A'J\;\), \(B'L//AA'\) \( \Rightarrow \dfrac{{IL}}{{IA}} = \dfrac{{IE}}{{IJ}} = \dfrac{{IB'}}{{IA'}} = \dfrac{1}{3}\)
\( \Rightarrow \dfrac{{{V_{I.ELB'}}}}{{{V_{I.JAA'}}}} = \dfrac{{IL}}{{IA}}.\dfrac{{IE}}{{IJ}}.\dfrac{{LE}}{{AJ}} = {\left( {\dfrac{1}{3}} \right)^3} = \dfrac{1}{{27}}\)
Do đó \({V_{I.ELB'}} = \dfrac{1}{{27}}{V_0}\)
Tương tự \({V_{J.MFD'}} = \dfrac{1}{{27}}{V_0}\)
Gọi \(A'B' = a,B'C' = b\), đường cao hạ từ \(A\) xuống \(\left( {A'B'C'D'} \right)\) là \(h\) thì \(IA' = \dfrac{3}{2}A'B' = \dfrac{{3a}}{2};\) \(A'J = \dfrac{3}{2}A'D' = \dfrac{{3b}}{2}\) và
\(V = {V_{ABCD.A'B'C'D'}}\)\( = {S_{A'B'C'D'}}h = abh.\sin \widehat {B'A'D'}\);
\({V_0} = \dfrac{1}{3}{S_{A'IJ}}.h\) \( = \dfrac{1}{3}.\left( {\dfrac{1}{2}.\dfrac{{3a}}{2}.\dfrac{{3b}}{2}\sin \widehat {B'A'D'}} \right)h\) \( = \dfrac{3}{8}abh.\sin \widehat {B'A'D'}\)
\( \Rightarrow \dfrac{{{V_0}}}{V} = \dfrac{3}{8} \Rightarrow {V_0} = \dfrac{{3V}}{8}\)
Vậy \({V_{(H)}} = {V_0} - \dfrac{2}{{27}}{V_0}\)\( = \dfrac{{25}}{{27}}{V_0} = \dfrac{{25}}{{27}}.\dfrac{{3V}}{8} = \dfrac{{25}}{{72}}V\)
\({V_{(H')}} = V - {V_{\left( H \right)}} = \dfrac{{47}}{{72}}V\) \( \Rightarrow \dfrac{{{V_{(H)}}}}{{{V_{(H')}}}} = \dfrac{{25}}{{47}}\).

