Đề bài
Cho tứ diện \(ABCD\). Gọi \(B'\) và \(C'\) lần lượt là trung điểm của \(AB\) và \(AC\). Tỉ số thể tích của khối tứ diện \(AB'C'D\) và khối tứ diện \(ABCD\) bằng:
A. \(\dfrac{1}{2}\) B. \(\dfrac{1}{4}\)
C. \(\dfrac{1}{6}\) D. \(\dfrac{1}{8}\)
Phương pháp giải - Xem chi tiết
Sử dụng công thức tính tỉ số thể tích hai khối chóp tam giác:
Xem tại đây.
Lời giải chi tiết
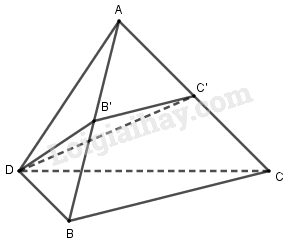
Ta có: \(\dfrac{{{V_{AB'C'D}}}}{{{V_{ABCD}}}} = \dfrac{{AB'}}{{AB}}.\dfrac{{AC'}}{{AC}}.\dfrac{{AD}}{{AD}}\) \( = \dfrac{1}{2}.\dfrac{1}{2}.1 = \dfrac{1}{4}\).
Chọn B.

