LG a
Khảo sát sự biến thiên và vẽ đồ thị (C) của hàm số : y=4x−5x−1
Lời giải chi tiết:
Tập xác định: D = R\{1}
Đạo hàm: y′=1(x−1)2
Bảng biến thiên:
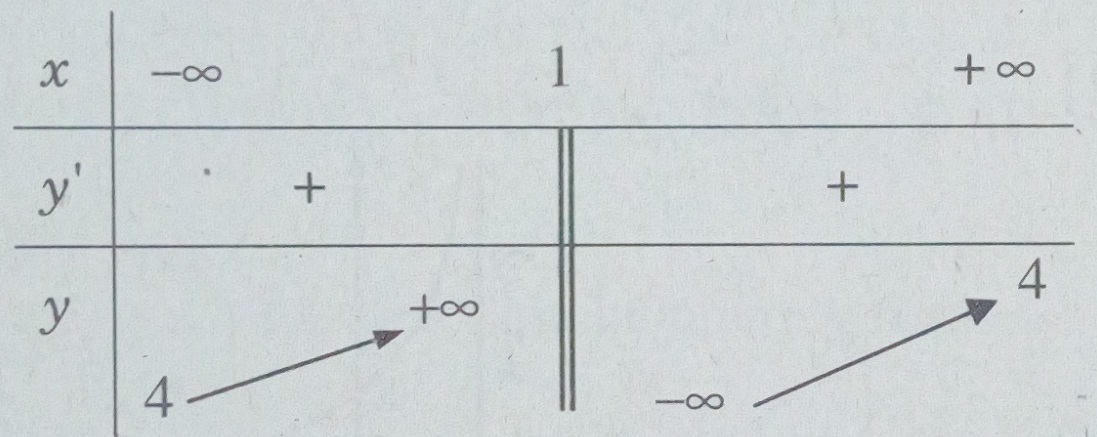
Các khoảng đồng biến là (−∞;1) và (1;+∞) :
Tiệm cận đứng x = 1 vì lim
Tiệm cận ngang y = 4 vì \mathop {\lim }\limits_{x \to \pm \infty } y = 4
Giao với các trục tọa độ: (0; 5) và ({5 \over 4};0)
Đồ thị
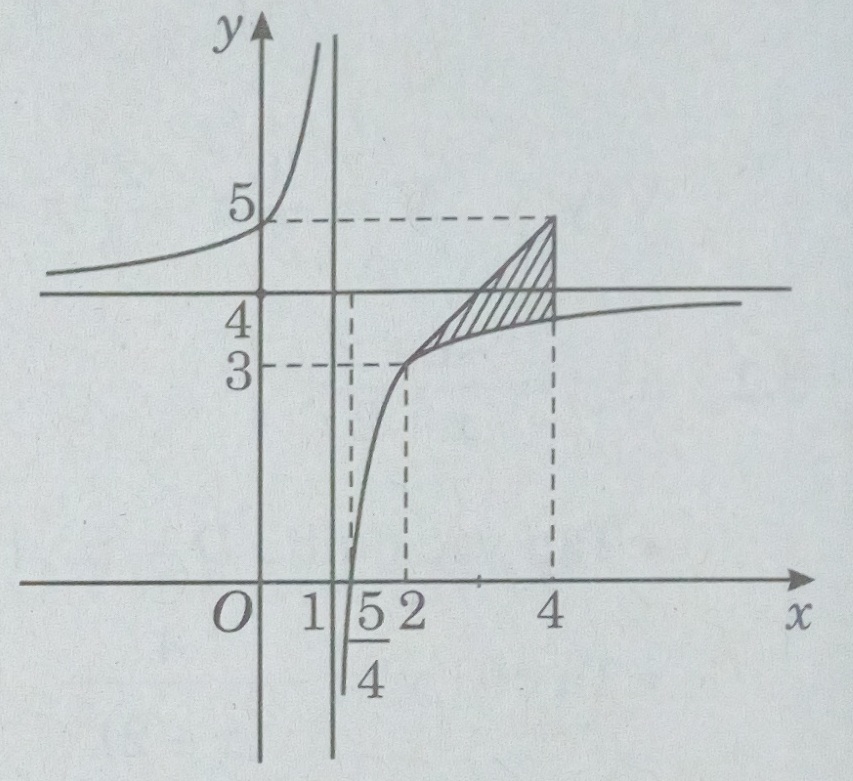
LG b
Tính diện tích hình phẳng giới hạn bởi (C), tiếp tuyến của (C) tại A(2; 3) và đường thẳng x = 4.
Lời giải chi tiết:
Ta có: y’(2) = 1. Phương trình tiếp tuyến là y = 1\left( {x - 2} \right) + 3 \Leftrightarrow y = x + 1
Diện tích của miền cần tìm là:
S = \int\limits_2^4 {\left( {x + 1 - \dfrac{{4x - 5}}{{x - 1}}} \right)dx} = \int\limits_2^4 {\left( {x + 1 - 4 + \dfrac{1}{{x - 1}}} \right)dx} = \int\limits_2^4 {\left( {x - 3 + \dfrac{1}{{x - 1}}} \right)dx} = \left. {\left( {\dfrac{{{x^2}}}{2} - 3x + \ln \left| {x - 1} \right|} \right)} \right|_2^4 = - 4 + \ln 3 + 4 = \ln 3
