Đề bài
Cho khối lập phương \(ABCD.A'B'C'D'\) cạnh bằng \(a\). Gọi \(M,N\) lần lượt là trung điểm của các cạnh \(AB,AD\). Mặt phẳng \(\left( {MB'D'N} \right)\) chia khối lập phương đã cho thành hai khối đa diện. Gọi \(\left( H \right)\) là khối đa diện chứa đỉnh \(A\). Thể tích của khối đa diện \(\left( H \right)\) bằng:
A. \(\dfrac{{{a^3}}}{9}\) B. \(\dfrac{{{a^3}}}{6}\)
C. \(\dfrac{{{a^3}}}{4}\) D. \(\dfrac{{7{a^3}}}{{24}}\)
Phương pháp giải - Xem chi tiết
- Kéo dài \(B'M,D'N\) cắt \(A'A\) tại \(S\).
- Tính thể tích khối chóp \(S.A'B'D'\) và \(S.AMN\) rồi suy ra đáp số.
Lời giải chi tiết
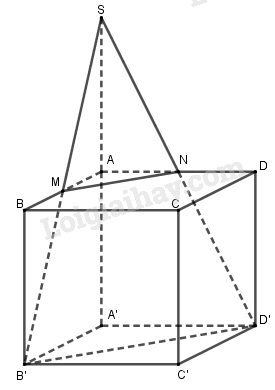
Kéo dài \(B'M,D'N\) cắt nhau tại \(S\).
Ta có: \(\left\{ \begin{array}{l}\left( {B'MND'} \right) \cap \left( {ABB'A'} \right) = B'M\\\left( {B'MND'} \right) \cap \left( {ADD'A'} \right) = D'N\\\left( {ABB'A'} \right) \cap \left( {ADD'A'} \right) = A'A\\B'M \cap D'N = \left\{ S \right\}\end{array} \right.\) \( \Rightarrow S \in A'A\).
Lại có \(\dfrac{{SA}}{{SA'}} = \dfrac{{SN}}{{SD'}} = \dfrac{{AN}}{{A'D'}} = \dfrac{1}{2}\)\( \Rightarrow SA = \dfrac{1}{2}SA'\) hay \(A\) là trung điểm của \(SA'\) hay \(SA = A'A = a\).
Ta có: \({V_{S.AMN}} = \dfrac{1}{3}SA.{S_{AMN}}\) \( = \dfrac{1}{3}a.\dfrac{1}{2}.\dfrac{a}{2}.\dfrac{a}{2} = \dfrac{{{a^3}}}{{24}}\).
\({V_{S.A'B'D'}} = \dfrac{1}{3}SA'.{S_{A'B'D'}}\) \( = \dfrac{1}{3}2a.\dfrac{1}{2}a.a = \dfrac{{{a^3}}}{3}\).
Vậy \({V_{AMN.A'B'D'}} = {V_{S.A'B'D'}} - {V_{S.AMN}}\) \( = \dfrac{{{a^3}}}{3} - \dfrac{{{a^3}}}{{24}} = \dfrac{{7{a^3}}}{{24}}\).
Chọn D.

