Đề bài
Cho hình chóp tam giác đều \(S.ABC\) có cạnh đáy bằng \(a\), diện tích một mặt bên bằng \(\dfrac{{5\sqrt 3 {a^2}}}{{12}}\). Thể tích của hình chóp bằng:
A. \(\dfrac{{\sqrt 6 }}{{24}}{a^3}\) B. \(\dfrac{{\sqrt 6 }}{{12}}{a^3}\)
C. \(\dfrac{{\sqrt 6 }}{4}{a^3}\) D. \(\dfrac{{\sqrt 2 }}{{12}}{a^3}\)
Phương pháp giải - Xem chi tiết
- Gọi \(O\) là tâm tam giác đáy, \(N\) là trung điểm \(AB\).
- Tính độ dài chiều cao và diện tích đáy.
- Tính thể tích theo công thức \(V = \dfrac{1}{3}Sh\).
Lời giải chi tiết
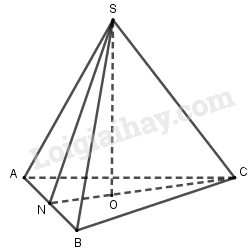
Tam giác \(ABC\) đều có \({S_{ABC}} = \dfrac{{{a^2}\sqrt 3 }}{4}\) và \(CN = \dfrac{{a\sqrt 3 }}{2}\) \( \Rightarrow ON = \dfrac{1}{3}CN = \dfrac{{a\sqrt 3 }}{6}\).
Tam giác \(SAB\) có \({S_{SAB}} = \dfrac{1}{2}AB.SN\) \( \Rightarrow SN = \dfrac{{2{S_{SAB}}}}{{AB}} = \dfrac{{2.\dfrac{{5\sqrt 3 {a^2}}}{{12}}}}{a} = \dfrac{{5\sqrt 3 a}}{6}\).
Tam giác \(SON\) vuông tại \(O\) có \(SO = \sqrt {S{N^2} - O{N^2}} \) \( = \sqrt {\dfrac{{75{a^2}}}{{36}} - \dfrac{{3{a^2}}}{{36}}} = a\sqrt 2 \)
Vậy thể tích khối chóp \({V_{S.ABC}} = \dfrac{1}{3}SO.{S_{ABC}}\) \( = \dfrac{1}{3}.a\sqrt 2 .\dfrac{{{a^2}\sqrt 3 }}{4} = \dfrac{{{a^3}\sqrt 6 }}{{12}}\).
Chọn B.

