Đề bài
Một hình trụ có các đáy là hai hình tròn tâm O và O’ bán kính r và có đường cao \(h = r\sqrt 2 \) . Gọi A là một điểm trên đường tròn tâm O và B là một điểm trên đường tròn tâm O’ sao cho OA vuông góc với O’B.
a) Chứng minh rằng các mặt bên của tứ diện OABO’ là những tam giác vuông. Tính thể tích của tứ diện này.
b) Gọi \((\alpha )\) là mặt phẳng qua AB và song song với OO’. Tính khoảng cách giữa trục OO’ và mặt phẳng \((\alpha )\).
c) Chứng minh rằng \((\alpha )\) tiếp xúc với mặt trụ trục OO’ có bán kính bằng \({{r\sqrt 2 } \over 2}\) dọc theo một đường sinh.
Phương pháp giải - Xem chi tiết
a) Sử dụng các kiến thức đã học để kiểm tra các tam giác mặt bên của tứ diện là hình tam gíac vuông.
Tính thể tích theo công thức \( V = \dfrac{1}{3}Sh\).
b) Góc giữa đường thẳng và mặt phẳng bằng góc giữa đường thẳng và hình chiếu của đường thẳng lên mặt phẳng đó.
c) Chỉ ra mặt trụ và kết luận.
Lời giải chi tiết
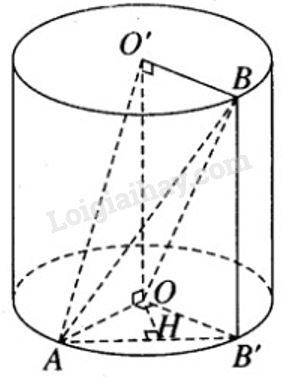
a) Vì trục OO’ vuông góc với các đáy nên \(\displaystyle {\rm{OO}}' \bot OA;{\rm{O}}O' \bot O'B\) .
Vậy các tam giác AOO’ và BO’O vuông tại O và O’.
Theo giả thiết ta có \(\displaystyle AO \bot O'B\) mà \(\displaystyle AO \bot {\rm{OO}}' = > AO \bot ({\rm{OO}}'B)\).
Do đó, \(\displaystyle AO \bot OB\) nên tam giác AOB vuông tại O.
Tương tự, ta chứng minh được tam giác AO’B vuông tại O’. Thể tích hình chóp OABO’ là: \(\displaystyle V = {1 \over 3}{S_{\Delta {\rm{OO}}'B}}.AO\)
Hay \(\displaystyle V = {1 \over 3}.{1 \over 2}OO'.O'B.AO \) \(\displaystyle = {1 \over 6}.r\sqrt 2 .{r^2} = {{\sqrt 2 } \over 6}{r^3}\)
b) Ta có \(\displaystyle (\alpha )\) là (ABB’).
Vì OO’ // \(\displaystyle (\alpha )\) nên khoảng cách giữa OO’ và \(\displaystyle (\alpha )\) bằng khoảng cách từ O đến \(\displaystyle (\alpha )\).
Dựng \(\displaystyle OH \bot AB'\) ta có \(\displaystyle OH \bot (\alpha )\) .
Tam giác OAB' vuông cân tại O có OA=OB'=r nên \(AB' = \sqrt {O{A^2} + OB{'^2}} \) \( = \sqrt {{r^2} + {r^2}} = r\sqrt 2 \)
\(OH \bot AB'\) nên OH cũng là đường trung tuyến của tam giác \( \Rightarrow OH = \frac{1}{2}AB' = \frac{{r\sqrt 2 }}{2}\)
Vậy khoảng cách cần tìm là \(\displaystyle OH = {{r\sqrt 2 } \over 2}\).
c) Đường tròn tâm O có bán kính bằng \(\displaystyle {{r\sqrt 2 } \over 2}\) tiếp xúc với AB’ tại H là trung điểm của AB’.
Do đó mặt phẳng \(\displaystyle (\alpha )\) song song với trục OO’ chứa tiếp tuyến của đường tròn đáy, nên \(\displaystyle (\alpha )\) tiếp xúc với mặt trụ dọc theo một đường sinh, với mặt trụ có trục OO’ và có bán kính đáy bằng \(\displaystyle {{r\sqrt 2 } \over 2}\).

