Đề bài
Hình chóp tam giác đều S.ABC có SA = SB = SC = a và có góc giữa mặt bên và mặt phẳng đáy bằng \(\alpha \). Tính diện tích xung quanh của hình trụ có đường tròn đáy là đường tròn nội tiếp tam giác đáy của hình chóp và có chiều cao bằng chiều cao của hình chóp. Các mặt bên SAB , SBC , SCA cắt hình trụ theo những giao tuyến như thế nào?
Phương pháp giải - Xem chi tiết
Sử dụng công thức tính diện tích xung quanh: \({S_{xq}} = 2\pi Rh\).
Lời giải chi tiết
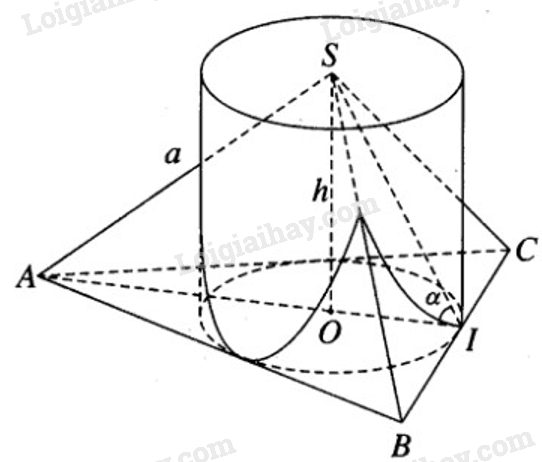
Theo giả thiết ta có tam giác đáy ABC là tam giác đều.
Gọi I là trung điểm của cạnh BC và O là tâm của tam giác đều ABC. Theo giả thiết ta có SA = a. Đặt OI = r , SO = h , ta có AO = 2r và \(\displaystyle \widehat {SIA} = \alpha \)
Do đó \(\displaystyle \left\{ {\matrix{{h = r\tan \alpha } \cr {{a^2} = {h^2} + 4{r^2}} \cr} } \right.\)
Vậy \(\displaystyle {a^2} = {r^2}{\tan ^2}\alpha + 4{r^2} = {r^2}({\tan ^2}\alpha + 4)\)
Ta suy ra \(\displaystyle r = {a \over {\sqrt {{{\tan }^2}\alpha + 4} }}\) và \(\displaystyle h = {{a.\tan \alpha } \over {\sqrt {{{\tan }^2}\alpha + 4} }}\)
Gọi Sxq là diện tích xung quanh của hình trụ ta có công thức \(\displaystyle {S_{xq}} = 2\pi rl\) trong đó \(\displaystyle r = {a \over {\sqrt {{{\tan }^2}\alpha + 4} }}\) và \(\displaystyle l = h = {{a\tan \alpha } \over {\sqrt {{{\tan }^2}\alpha + 4} }}\)
Vậy \(\displaystyle {S_{xq}} = 2\pi .{{{a^2}\tan \alpha } \over {{{\tan }^2}\alpha + 4}}\)
Các mặt bên SAB, SBC, SCA là những phần của ba mặt phẳng không song song với trục và cũng không vuông góc với trục nên chúng cắt mặt phẳng xung quanh của hình trụ theo những cung elip. Các cung này có hình chiếu vuông góc trên mặt phẳng (ABC) tạo nên đường tròn đáy của hình trụ.

