Đề bài
Chia một khối tứ diện đều thành bốn tứ diện bằng nhau.
Phương pháp giải - Xem chi tiết
- Gọi \(G\) là trọng tâm tứ diện đều \(ABCD\).
- Chứng minh các hình tứ diện có đỉnh là \(G\) và đáy và các mặt bên của tứ diện đã cho bằng nhau.
Lời giải chi tiết
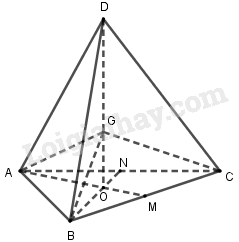
Xét tứ diện đều \(ABCD\). Gọi \(G\) là giao điểm của các đường thẳng nối đỉnh với trọng tâm của mặt đối diện.
Khi đó dễ thấy các tứ diện \(GABC,GBCD,GCDA,GDAB\) bằng nhau.
Thật vậy, các tứ diện trên đều có đáy là các tam giác đều có cạnh bằng nhau, các cạnh bên \(GA = GB = GC = GD\).
Vậy ta đã chia được tứ diện đều thành \(4\) tứ diện bằng nhau.

