Cho hàm số: \(y = f\left( x \right) = {x^4}-2m{x^2} + {m^3}-{m^2}\)
LG a
Khảo sát sự biến thiên và vẽ đồ thị của hàm số khi \(m = 1\).
Phương pháp giải:
- Thay \(m\) được hàm số cần khảo sát.
- Khảo sát tóm tắt:
+ Tìm TXĐ.
+ Xét sự biến thiên.
+ Vẽ đồ thị.
Lời giải chi tiết:
Với \(m = 1\) ta được hàm số \(y = {x^4} - 2{x^2}\).
TXĐ: \(D = \mathbb{R}\)
Giới hạn: \(\mathop {\lim }\limits_{x \to \pm \infty } y = + \infty \)
Chiều biến thiên:
Có \(y' = 4{x^3} - 4x = 4x({x^2} - 1)\); \(y' = 0 \Leftrightarrow \left[ \begin{array}{l}x = - 1\\x = 0\\x = 1\end{array} \right.\)
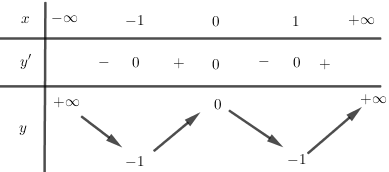
Hàm số đồng biến trên các khoảng \(\left( { - 1;0} \right)\) và \(\left( {1; + \infty } \right)\)
Nghịch biến trên các khoảng \(\left( { - \infty ; - 1} \right)\) và \(\left( {0;1} \right)\).
Hàm số đạt cực đại tại \(x = 0\) và \({y_{CD}} = 0\)
Hàm số đạt cực tiểu tại \(x = \pm 1\) và \({y_{CT}} = - 1\).
Bảng biến thiên:
Đồ thị:
+) Điểm uốn: \(y'' = 12{x^2} - 4;\)
\(y'' = 0 \Leftrightarrow 12{x^2} - 4 = 0\) \( \Leftrightarrow {x^2} = \frac{1}{3} \Leftrightarrow x = \pm \frac{1}{{\sqrt 3 }}\)
Đồ thị hàm số nhận các điểm \(\left( { \pm \frac{1}{{\sqrt 3 }}; - \frac{5}{9}} \right)\) làm điểm uốn.
+) Cắt trục Oy tại \(\left( {0;0} \right)\)
+) Cắt trục Ox tại các điểm \(\left( {0;0} \right),\left( { \pm \sqrt 2 ;0} \right)\)

LG b
Xác định \(m\) để đồ thị \(\left( {{C_m}} \right)\) của hàm số đã cho tiếp xúc với trục hoành tại hai điểm phân biệt.
Phương pháp giải:
Đồ thị hàm số tiếp xúc trục hoành tại hai điểm phân biệt nếu và chỉ nếu hàm số đã cho có hai điểm cực tiểu và \({y_{CT}} = 0\).
Lời giải chi tiết:
Để \(\left( {{C_m}} \right)\) tiếp xúc với trục hoành tại hai điểm phân biệt thì điều kiện cần và đủ là hàm số đã cho có hai điểm cực tiểu, \(1\) điểm cực đại và \({y_{CT}} = 0\).
Ta có: \(y' = 4{x^3} - 4mx = 4x\left( {{x^2} - m} \right)\); \(y' = 0 \Leftrightarrow \left[ \begin{array}{l}x = 0\\{x^2} = m\end{array} \right.\).
Để hàm số có hai điểm cực tiểu, một điểm cực đại thì phương trình \({x^2} = m\) có hai nghiệm phân biệt khác \(0\)
+) Nếu m ≤ 0 thì x2 – m ≥ 0 với mọi x nên đồ thị không thể tiếp xúc với trục Ox tại hai điểm phân biệt.
+) Nếu m > 0 thì y’ = 0 khi x = 0; x = √m hoặc x = -√m.
Khi đó hàm số có hai điểm cực tiểu là \(x = \sqrt m \) và \(x = - \sqrt m \);
\( \Rightarrow {y_{CT}} = f\left( { \pm \sqrt m } \right)\) \( = {m^2} - 2{m^2} + {m^3} - {m^2} = {m^3} - 2{m^2}\)
\({y_{CT}} = 0 \Leftrightarrow {m^3} - 2{m^2} = 0\) \( \Leftrightarrow \left[ \begin{array}{l}m = 0\left( {KTM} \right)\\m = 2\left( {TM} \right)\end{array} \right.\).
Vậy \(m = 2\) là giá trị cần tìm.

