Đề bài
Cho hình lăng trụ ngũ giác \(ABCDE.A'B'C'D'E'\). Gọi \(A'',B'',C'',D'',E''\) lần lượt là trung điểm các cạnh \(AA',BB',CC',DD',EE'\). Tỉ số thể tích giữa khối lăng trụ \(ABCDE.A''B''C''D''E''\) và khối lăng trụ \(ABCDE.A'B'C'D'E'\) bằng:
A. \(\dfrac{1}{2}\) B. \(\dfrac{1}{4}\)
C. \(\dfrac{1}{8}\) D. \(\dfrac{1}{{10}}\)
Phương pháp giải - Xem chi tiết
Viết công thức tính thể tích mỗi khối lăng trụ, từ đó suy ra tỉ số thể tích.
Lời giải chi tiết
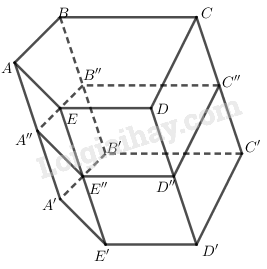
Gọi \(h\) là chiều cao của khối lăng trụ.
Khi đó \(d\left( {\left( {ABCDE} \right),\left( {A'B'C'D'E'} \right)} \right) = h\) \( \Rightarrow d\left( {\left( {ABCDE} \right),\left( {A''B''C''D''E''} \right)} \right) = \dfrac{h}{2}\)
Thể tích khối lăng trụ \(ABCDE.A'B'C'D'E'\) là \({V_1} = {S_{ABCD}}.h\).
Thể tích khối lăng trụ \(ABCDE.A''B''C''D''E''\) là \({V_2} = {S_{ABCD}}.\dfrac{h}{2}\).
Vậy \(\dfrac{{{V_2}}}{{{V_1}}} = \dfrac{1}{2}\).
Chọn A.

