Đề bài
Chia hình chóp tứ giác đều thành tám hình chóp bằng nhau.
Phương pháp giải - Xem chi tiết
Chia đáy hình chóp thành \(8\) tam giác bằng nhau rồi chứng minh các hình chóp có đỉnh là đỉnh của hình chóp ban đầu và đáy là mỗi tam giác vừa có được thì bằng nhau.
Sử dụng lý thuyết: Hai tứ diện có các cạnh tương ứng bằng nhau thì bằng nhau
Lời giải chi tiết
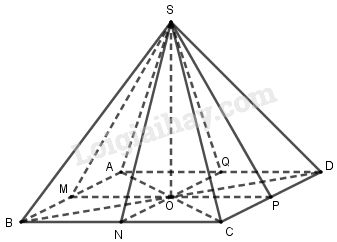
Gọi \(O = AC \cap BD\), các điểm \(M,N,P,Q\) lần lượt là trung điểm của mỗi đoạn thẳng \(AB,BC,CD,DA\).
Khi đó các tam giác \(AOM,BOM,BON,CON,\) \(COP,DOP,DOQ,AOQ\) bằng nhau.
Ta chứng minh các hình chóp \(S.AOM,S.BOM,S.BON,S.CON,\) \(S.COP,S.DOP,S.DOQ,S.AOQ\) bằng nhau.
Xét hai hình chóp \(S.AOM\) và \(S.BOM\) có \(SA = SB,AO = BO,AM = BM,\) \(SO\) chung và \(SM\) chung, \(OM\) chung.
Do đó hai tứ diện có các cạnh tương ứng bằng nhau thì bằng nhau.
Tương tự ta có \(8\) hình chóp bằng nhau.

