Đề bài
Cho hình chóp \(S.ABC\) có \(SA\) vuông góc với đáy. Mặt phẳng qua \(A\) và vuông góc với \(SC\) cắt \(SB,SC\) lần lượt tại \(M,N\). Biết rằng \(SA = AC = 5\), \(AB = 3,BC = 4\). Thể tích khối chóp \(S.AMN\) bằng
A. \(\dfrac{{125}}{{68}}\) B. \(\dfrac{{125}}{{34}}\)
C. \(\dfrac{{175}}{{34}}\) D. \(\dfrac{{125}}{{17}}\)
Phương pháp giải - Xem chi tiết
- Tính tỉ số diện tích hai tam giác \(SMN\) và \(SBC\).
- Từ đó suy ra tỉ số thể tích khối chóp \(S.AMN\) so với \(S.ABC\).
- Tính \({V_{S.ABC}}\) và kết luận.
Lời giải chi tiết
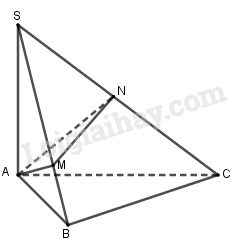
Ta có: \(SC \bot \left( {AMN} \right) \Rightarrow \left\{ \begin{array}{l}SC \bot AM\\SC \bot MN\end{array} \right.\).
Tam giác \(ABC\) có:
\(A{C^2} =5^2=25\)
\(A{B^2} + B{C^2}=3^2+4^2=25 \)
nên \(AC^2=AB^2+BC^2\) hay tam giác ABC vuông tại \(B\).
Suy ra \(AB \bot BC\), mà \(SA \bot BC\) nên \(BC \bot \left( {SAB} \right) \Rightarrow BC \bot SB\).
Xét tam giác SMN và SCB có: \(\widehat {SNM} = \widehat {SBC} = {90^0}\) và chung góc S
\( \Rightarrow \Delta SMN \backsim \Delta SCB\left( {g - g} \right)\) \( \Rightarrow \dfrac{{{S_{SMN}}}}{{{S_{SCB}}}} = {\left( {\dfrac{{SN}}{{SB}}} \right)^2}\)
Tam giác \(SAC\) vuông cân tại \(A\) có \(AN \bot SC\) \( \Rightarrow SN = \dfrac{1}{2}SC = \dfrac{1}{2}\sqrt {{5^2} + {5^2}} = \dfrac{{5\sqrt 2 }}{2}\).
Tam giác \(SAB\) có \(SA = 5,AB = 3 \Rightarrow SB = \sqrt {34} \)
\( \Rightarrow \dfrac{{{S_{SMN}}}}{{{S_{SCB}}}} = {\left( {\dfrac{{SN}}{{SB}}} \right)^2} = \dfrac{{25}}{{68}}\)\( \Rightarrow \dfrac{{{V_{S.AMN}}}}{{{V_{S.ABC}}}} = \dfrac{{25}}{{68}}\).
Mà \({V_{S.ABC}} = \dfrac{1}{3}SA.{S_{ABC}} \) \(= \dfrac{1}{3}.5.\dfrac{1}{2}.3.4 = 10\) nên \({V_{S.AMN}} = \dfrac{{25}}{{68}}.10 = \dfrac{{125}}{{34}}\).
Chọn B.

