Xét sự đồng biến, nghịch biến của các hàm số:
LG câu a
a) y=3x2−8x3
Phương pháp giải:
- Tính y′.
- Tìm nghiệm của phương trình y′=0.
- Xét dấu y′ và kết luận.
Lời giải chi tiết:
TXĐ: R
y′=6x−24x2=6x(1−4x)
y′=0⇔[x=0x=14
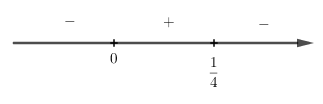
Xét dấu y′:
Ta thấy, y′>0⇔0<x<14 nên hàm số đồng biến trên khoảng (0;14).
y′<0⇔[x>14x<0 nên hàm số nghịch biến trên các khoảng (−∞;0) và (14;+∞).
LG câu b
b) y=16x+2x2−163x3−x4
Phương pháp giải:
- Tính y′.
- Tìm nghiệm của phương trình y′=0.
- Xét dấu y′ và kết luận.
Lời giải chi tiết:
TXĐ: R
y′=16+4x−16x2−4x3 =−4(x+4)(x2−1)
y′=0⇔[x=−4x=±1
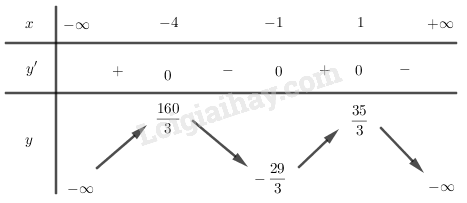
Bảng biến thiên:
Vậy hàm số đã cho đồng biến trên các khoảng (−∞;−4) và (−1;1), nghịch biến trên các khoảng (−4;−1) và (1;+∞).
LG câu c
c) y=x3−6x2+9x
Phương pháp giải:
- Tính y′.
- Tìm nghiệm của phương trình y′=0.
- Xét dấu y′ và kết luận.
Lời giải chi tiết:
TXĐ: R
y′=3x2−12x+9
y'=0 <=> [x=1x=3
y′>0⇔[x>3x<1 nên hàm số đồng biến trên các khoảng (−∞;1) và (3;+∞).
y′<0⇔1<x<3 nên hàm số nghịch biến trên khoảng (1;3).
LG câu d
d) y=x4+8x2+5
Phương pháp giải:
- Tính y′.
- Tìm nghiệm của phương trình y′=0.
- Xét dấu y′ và kết luận.
Lời giải chi tiết:
TXĐ: R
y′=4x3+16x=4x(x2+4)
y′=0⇔x=0
y′>0⇔x>0 nên hàm số đồng biến trên khoảng (0;+∞).
y′<0⇔x<0 nên hàm số nghịch biến trên khoảng (−∞;0).
