Đề bài
Cho hình lăng trụ đứng \(ABC.A’B’C’\) có đáy là tam giác vuông ở \(B\), \(AB = BC = AA’\). Hãy chia lăng trụ đó thành ba tứ diện bằng nhau.
Phương pháp giải - Xem chi tiết
Sử dụng định nghĩa đa diện bằng nhau: Hai đa diện được gọi là bằng nhau nếu có một phép dời hình biến đa diện này thành đa diện kia.
Lời giải chi tiết
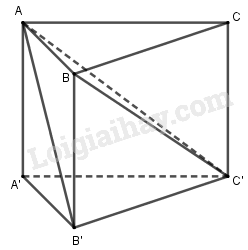
Chia lăng trụ đã cho thành ba tứ diện: \(ABCC’ , ABB’C’\) và \(AA’B’C’\).
Ta có: \(\left\{ \begin{array}{l}AB \bot BC\\AB \bot BB'\end{array} \right.\) \( \Rightarrow AB \bot \left( {BCC'B'} \right) \Rightarrow AB \bot B'C\) (1)
Hình chữ nhật \(BCC'B'\) có \(BC = BB'\) nên là hình vuông
Do đó \(B'C \bot BC'\) (2)
Từ (1) và (2) suy ra \(B'C \bot \left( {ABC'} \right)\)
Mà \(BCC'B'\) là hình vuông nên B’C cắt BC’ tại trung điểm của B’C
Suy ra (ABC’) là mp trung trực của B’C.
\(\begin{array}{l}
\Rightarrow {D_{\left( {ABC'} \right)}}\left( C \right) = B'\\
{D_{\left( {ABC'} \right)}}\left( A \right) = A\\
{D_{\left( {ABC'} \right)}}\left( B \right) = B\\
{D_{\left( {ABC'} \right)}}\left( {C'} \right) = C'
\end{array}\)
\( \Rightarrow \) Phép đối xứng qua mặt phẳng \( (ABC’) \) biến tứ diện \(ABCC’\) thành tứ diện \(ABB’C’\).
Tương tự, phép đối xứng qua mặt phẳng \( (AB’C’) \) biến tứ diện \(ABB’C’\) thành tứ diện \(AA’B’C’\).
Vậy ba tứ diện đó bằng nhau.

