LG a
Khảo sát sự biến thiên và vẽ đồ thị của hàm số f(x) = 2x3 – 3x2 – 12x – 10
Phương pháp giải:
- Tìm TXĐ.
- Tính đạo hàm, lập bảng biến thiên.
- Vẽ đồ thị.
Lời giải chi tiết:
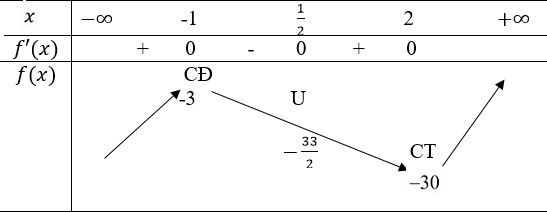
TXD: D=R
f ’(x) = 6(x2 – x – 2)
f′(x)=0⇔[x=−1x=2
Hàm số đạt cực đại tại x=1;yCĐ=−3
Hàm số đạt cực tiểu tại x=2;yCĐ=−30
lim
Ta có bảng biến thiên:
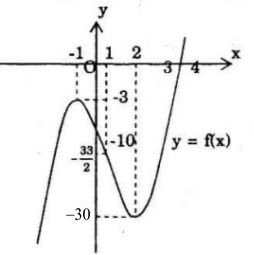
Đồ thị
LG b
Chứng minh rằng phương trình 2x3 – 3x2 – 12x – 10 = 0 có nghiệm thực duy nhất.
Phương pháp giải:
Sử dụng tương giao đồ thị, số nghiệm của phương trình bằng số giao điểm của đồ thị hàm số với trục hoành.
Lời giải chi tiết:
Đồ thị hàm số y = 2x3 – 3x2 – 12x – 10 cắt trục hoành tại một điểm duy nhất nên phương trình đã cho có nghiệm thực duy nhất.
LG c
Gọi nghiệm thực duy nhất của hàm số là α. Chứng ming rằnh 3,5 < α < 3,6.
Phương pháp giải:
Sử dụng định lí: Hàm số f(x) liên tục trên (a;b) và f(a).f(b)<0 thì tồn tại ít nhất một điểm c trong (a;b) sao cho f(c)=0.
Lời giải chi tiết:
Ta có: f(3, 5).f(3, 6) < 0 và hàm số liên tục trên (3,5;3,6).
Vì vậy, phương trình có nghiệm α duy nhất thỏa mãn điều kiện 3,5 < α < 3,6.

