Trên mặt mỗi chiếc radio đều có các vạch chia để người sử dụng dẽ dàng chọn đúng sóng
Radio cần tìm. Biết rằng vạch chia ở vị trí cách vạch tận cùng bên trái một khoảng d (cm) thì ứng tần số \(F = k{a^{d\,}}\,\,\left( {kHz} \right)\), trong đó k và a là hai hằng số được chọn sao cho vạch tận cùng trên trái ứng với tần số 53 kHz, vạch tận cùng bên phải ứng với tần số 160 kHz, và hai vạch này cách nhau 12 cm.
LG a
Hãy tính k và a (tính a chính xác đến hàng phần nghìn).
Lời giải chi tiết:
Ta có với d = 0 thì F = 53
Do đó \(53 = k.{a^0} \Leftrightarrow k = 53\)
Với d = 12 thì F =160
Do đó \(160 = k.{a^{12}} = 53.{a^{12}} \)\( \Leftrightarrow {a^{12}} = \frac{{160}}{{53}}\)
\(\Leftrightarrow a = \root {12} \of {{{160} \over {53}}} \approx 1,096\)
LG b
Giả sử đã cho F, hãy giải phương trình \(F = k{a^{d}}\) với ẩn d.
Lời giải chi tiết:
\(\begin{array}{l}
k{a^d} = F \Leftrightarrow {a^d} = \frac{F}{k}\\
\Leftrightarrow d = {\log _a}\left( {\frac{F}{k}} \right)\\
\Leftrightarrow d = \frac{{\log \left( {\frac{F}{k}} \right)}}{{\log a}}\\
\Leftrightarrow d = \frac{{\log F - \log k}}{{\log a}}\\
\Rightarrow d \approx \frac{{\log F - \log 53}}{{\log 1,096}}
\end{array}\)
LG c
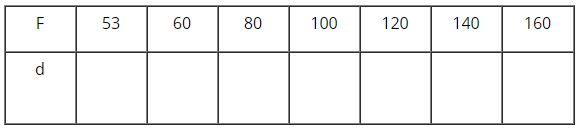
Áp dụng kết quả của b), hãy điền vào ô trống trong bảng sau (kết quả tính chính xác đến hàng phần trăm).
Lời giải chi tiết:
