LG a
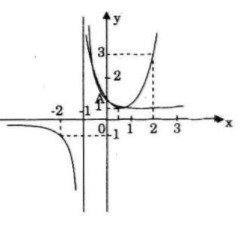
Vẽ đồ thị (P) của hàm số y=x2−x+1 và đồ thị (H) của hàm số y=1x+1.
Lời giải chi tiết:
Vẽ (P):
(P) là parabol có đỉnh (12;34), bề lõm hướng lên trên, đi qua điểm (0;1), (1;1)
Vẽ (H):
y′=−1(x+1)2<0,∀x≠−1 nên hàm số nghịch biến trên các khoảng (−∞;−1) và (−1;+∞)
Đồ thị có TCĐ x=−1, TCN y=0
Đi qua các điểm (0;1),(−2;−1)
LG b
Tìm giao điểm của hai đường cong (P) và (H). Chứng minh rằng hai đường cong đó có tiếp tuyến chung tại giao điểm của chúng.
Lời giải chi tiết:
Hoành độ giao điểm của parabol (P) và hypebol (H) là nghiệm của phương trình:
x2−x+1=1x+1 ⇒(x+1)(x2−x+1)=1
⇔x3+1=1⇔x=0
⇒y(0)=1
Giao điểm của (P) và (H) là A(0;1)
Đặt f(x)=x2−x+1;g(x)=1x+1
Ta có: f′(x)=2x−1;g′(x)=−1(x+1)2
f′(0)=g′(0)=−1
Suy ra (P) và (H) có tiếp tuyến chung tại A nên (P) và (H) tiếp xúc nhau tại điểm A.
Khi đó tiếp tuyến chung của (P) và (H) tại A(0;1) có hệ số góc k=-1 nên có phương trình:
y=-1(x-0)+1 hay y=-x+1.
Chú ý:
Việc tìm giao điểm có thể suy ra từ việc quan sát đồ thị ta cũng thấy giao điểm là (0;1).
LG c
Xác định các khoảng trên đó (P) nằm phía trên hoặc phía dưới (H).
Lời giải chi tiết:
Xét hiệu f(x)−g(x)=x2−x+1−1x+1 =x3x+1
Bảng xét dấu f(x) – g(x)
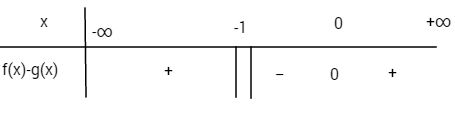
Từ bảng xét dấu ta thấy,
f(x)>g(x) ⇔f(x)−g(x)>0 ⇔[x>0x<−1
Do đó, trên các khoảng (−∞;−1) và (0;+∞) thì (P) nằm phía trên (H).
f(x)<g(x) ⇔f(x)−g(x)<0 ⇔−1<x<0 nên trên khoảng (−1;0) thì (P) nằm phía dưới (H).

