Đề bài
Cho hình phẳng A giới hạn bởi các đường y=0,x=4, và y=√x−1. Tính thể tích của khối tròn xoay tạo thành khi quay hình A quanh trục hoành.
Phương pháp giải - Xem chi tiết
Sử dụng công thức V=πb∫af2(x)dx
Lời giải chi tiết
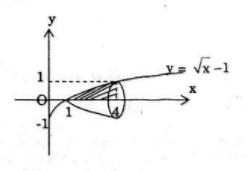
Hoành độ giao điểm của đường thẳng với trục hoành
√x−1=0⇔x=1V=π4∫1(√x−1)2dx=π4∫1(x−2√x+1)dx=π(x22−2x3232+x)|41=π(x22−43x√x+x)|41=7π6

