Tính diện tích hình phẳng giới hạn bởi:
LG a
Đồ thị các hàm số \(y = x, y = 1\) và \(y = {{{x^2}} \over 4}\) trong miền \(x \ge 0,y \le 1.\)
Phương pháp giải:
Dựng hình, tính diện tích miền cần tính và kết luận.
Lời giải chi tiết:
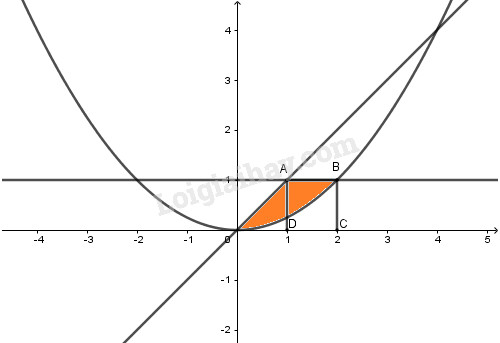
Diện tích hình thang \(OABC\) là:
\({S_1} = (2 + 1){1 \over 2} = {3 \over 2}\)
Diện tích tam giác cong \(OBC\) là hình phẳng giới hạn bởi: \(y = 0,x = 2,y = {{{x^2}} \over 4}\) là:
\({S_2} = \int\limits_0^2 {{{{x^2}} \over 4}} dx = \left. {{{{x^3}} \over {12}}} \right|_0^2 = {2 \over 3}\)
Diện tích cần tìm là \(S = {S_1} - {S_2} = {3 \over 2} - {2 \over 3} = {5 \over 6}\).
Cách 2:
Diện tích hình phẳng cần tìm chính là tổng diện tích tam giác cong OAD và tam giác cong ADB.
Diện tích tam giác cong OAD là:
\({S_{OAD}} = \int\limits_0^1 {\left( {x - \dfrac{{{x^2}}}{4}} \right)dx} \) \( = \left. {\left( {\dfrac{{{x^2}}}{2} - \dfrac{{{x^3}}}{{12}}} \right)} \right|_0^1 = \dfrac{5}{{12}} - 0 = \dfrac{5}{{12}}\)
Diện tích tam giác cong ADB là:
\({S_{ADB}} = \int\limits_1^2 {\left( {1 - \dfrac{{{x^2}}}{4}} \right)dx} \) \( = \left. {\left( {x - \dfrac{{{x^3}}}{{12}}} \right)} \right|_1^2 = \dfrac{4}{3} - \dfrac{{11}}{{12}} = \dfrac{5}{{12}}\)
Vật diện tích hình phẳng cần tìm là:
\(\dfrac{5}{{12}} + \dfrac{5}{{12}} = \dfrac{5}{6}\)
Cách 3.
Ta có: \(y = \dfrac{{{x^2}}}{4} \Leftrightarrow {x^2} = 4y\) \( \Leftrightarrow x = 2\sqrt y \) (do ta chỉ xét miền \(x \ge 0\))
Gọi hình phẳng đã cho là hình phẳng giới hạn bởi đường cong có phương trình x=2 √y, đường thẳng x = y và y = 0 và đường thẳng y = 1. Diện tích cần tìm là:
\(S = \int\limits_0^1 {\left( {2\sqrt y - y} \right)dy}\) \( = \left. {\left( {2.\dfrac{{{y^{\dfrac{3}{2}}}}}{{\dfrac{3}{2}}} - \dfrac{{{y^2}}}{2}} \right)} \right|_0^1\) \( = \left. {\left( {\dfrac{4}{3}y\sqrt y - \dfrac{{{y^2}}}{2}} \right)} \right|_0^1 = \dfrac{5}{6} - 0 = \dfrac{5}{6}\)
LG b
Đồ thị hai hàm số \(y = {x^4} - 4{x^2} + 4,y = {x^2}\), trục tung và đường thẳng \(x = 1\)
Phương pháp giải:
Tính diện tích hình phẳng giới hạn bởi các đồ thị hàm số \(y = f\left( x \right),y = g\left( x \right),\) \(x = a,x = b\).
+) B1: Tìm nghiệm \(a \le {x_1} < {x_2} < ... < {x_n} \le b\) của phương trình hoành độ giao điểm \(f\left( x \right) = g\left( x \right)\).
+) B2: Tính diện tích theo công thức:
\(S = \int\limits_a^b {\left| {f\left( x \right) - g\left( x \right)} \right|dx} \)
\( = \int\limits_a^{{x_1}} {\left| {f\left( x \right) - g\left( x \right)} \right|dx} \) \( + \int\limits_{{x_1}}^{{x_2}} {\left| {f\left( x \right) - g\left( x \right)} \right|dx} \) \( + ... + \int\limits_{{x_{n - 1}}}^{{x_n}} {\left| {f\left( x \right) - g\left( x \right)} \right|dx} \) \( + \int\limits_{{x_n}}^b {\left| {f\left( x \right) - g\left( x \right)} \right|dx} \)
\( = \left| {\int\limits_a^{{x_1}} {\left[ {f\left( x \right) - g\left( x \right)} \right]dx} } \right|\)\( + \left| {\int\limits_{{x_1}}^{{x_2}} {\left[ {f\left( x \right) - g\left( x \right)} \right]dx} } \right|\) \( + ... + \left| {\int\limits_{{x_{n - 1}}}^{{x_n}} {\left[ {f\left( x \right) - g\left( x \right)} \right]dx} } \right|\) \( + \left| {\int\limits_{{x_n}}^b {\left[ {f\left( x \right) - g\left( x \right)} \right]dx} } \right|\)
Lời giải chi tiết:
Cách 1:
Phương trình hoành độ giao điểm của hai đồ thị là:
\({x^4} - 4{x^2} + 4 = {x^2} \Leftrightarrow \left[ \matrix{
{x^2} = 1 \hfill \cr
{x^2} = 4 \hfill \cr} \right. \) \(\Leftrightarrow \left[ \matrix{
x = \pm 1 \hfill \cr
x = \pm 2 \hfill \cr} \right.\)
Ta có: \(-2<-1<0<1<2\) nên
\(S=\int\limits_{0}^{1}{\left| {{x}^{4}}-4{{x}^{2}}+4-{{x}^{2}} \right|dx}\) \(=\int\limits_{0}^{1}{\left| {{x}^{4}}-5{{x}^{2}}+4 \right|dx}\) \(=\left| \int\limits_{0}^{1}{\left( {{x}^{4}}-5{{x}^{2}}+4 \right)dx} \right|\) \(=\left| \left. \left( \dfrac{{{x}^{5}}}{5}-\dfrac{5{{x}^{3}}}{3}+4x \right) \right|_{0}^{1} \right|\) \(=\left| \dfrac{38}{15} \right|=\dfrac{38}{15}\)
Cách 2:
Phương trình hoành độ giao điểm của hai đồ thị là:
\({x^4} - 4{x^2} + 4 = {x^2} \Leftrightarrow \left[ \matrix{
{x^2} = 1 \hfill \cr
{x^2} = 4 \hfill \cr} \right. \) \(\Leftrightarrow \left[ \matrix{
x = \pm 1 \hfill \cr
x = \pm 2 \hfill \cr} \right.\)
Ta có:
\(\eqalign{
& S = \int\limits_0^1 {\left| {{x^4} - 4{x^2} + 4 - {x^2}} \right|} dx \cr &= \int\limits_0^1 {\left| {{x^4} - 5{x^2} + 4} \right|} dx \cr
& = \int\limits_0^1 {({x^4} - 5{x^2}} + 4)dx \cr &= \left. {\left( {{{{x^5}} \over 5} - {{5{x^3}} \over 3} + 4x} \right)} \right|_0^1 = {{38} \over {15}} \cr} \)
LG c
Đồ thị các hàm số \(y = {x^2},y = 4x - 4\) và \(y = -4x – 4\).
Phương pháp giải:
Dựng hình suy ra các công thức tính diện tích.
Lời giải chi tiết:
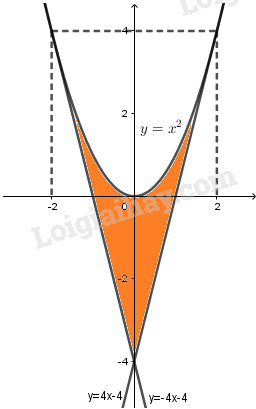
Phương trình hoành độ giao điểm của đồ thị hàm số \(y = {x^2}\) và đường thẳng \(y = 4x – 4\) là:
\(\eqalign{
& {x^2} = 4x - 4 \Leftrightarrow {x^2} - 4x + 4 = 0 \cr
& \Leftrightarrow {(x - 2)^2} = 0 \Leftrightarrow x = 2. \cr} \)
Phương trình hoành độ giao điểm của đồ thị hàm số \(y = {x^2}\) và đường thẳng
\(y = -4x – 4\) là:
\(\eqalign{
& {x^2} = - 4x - 4 \Leftrightarrow {x^2} + 4x + 4 = 0 \cr
& \Leftrightarrow {(x + 2)^2} = 0 \Leftrightarrow x = - 2. \cr} \)
\(\eqalign{
& S = \int\limits_{ - 2}^0 {\left| {{x^2} - \left( { - 4x - 4} \right)} \right|dx} \cr &+ \int\limits_0^2 {\left| {{x^2} - \left( {4x - 4} \right)} \right|dx}\cr & = \int\limits_{ - 2}^0 {({x^2} + 4x + 4)} dx \cr &+ \int\limits_0^2 {({x^2} - 4x + 4)} dx \cr
& = \left. {\left( {{{{x^3}} \over 3} + 2{x^2} + 4x} \right)} \right|_{ - 2}^0 \cr &+ \left. {\left( {{{{x^3}} \over 3} - 2{x^2} + 4x} \right)} \right|_0^2 \cr &= {8 \over 3} + {8 \over 3} = {{16} \over 3} \cr} \)
Cách khác:
Do tính đối xứng qua Oy của parabol y=x2 nên diện tích hình phẳng cần tìm bằng 2 lần diện tích tam giác cong giới hạn bởi đồ thị hàm số \(y = {x^2}\), trục tung, đường thẳng \(y = 4x - 4\). Khi đó,
\(S = 2\int\limits_0^2 {\left( {{x^2} - 4x + 4} \right)dx} \) \( = 2\left. {\left( {\dfrac{{{x^3}}}{3} - 2{x^2} + 4x} \right)} \right|_0^2\) \( = 2\left( {\dfrac{8}{3} - 0} \right) = \dfrac{{16}}{3}\)

