Cho hàm số : y=f(x)=x+1x
LG a
Khảo sát sự biến thiên và vẽ đồ thị (C) của hàm số.
Lời giải chi tiết:
Tập xác định: D=R∖{0}
y′=1−1x2=x2−1x2y′=0⇔x=±1
Hàm số đồng biến trên các khoảng: (−∞;−1),(1;+∞)
Hàm số nghịch biến trên các khoảng: (−1;0),(0;1)
+) Cực trị:
Hàm số đạt cực đại tại: x=−1;y(−1)=−2
Hàm số đạt cực tiểu tại: x=1;y(1)=2
+) Giới hạn:
lim
Tiệm cận đứng: x=0
\mathop {\lim }\limits_{x \to \pm \infty } y = \pm \infty
\mathop {\lim }\limits_{x \to \infty } (y - x) = \mathop {\lim }\limits_{x \to \infty } {1 \over x} = 0
Tiệm cận xiên: y=x
Bảng biến thiên:
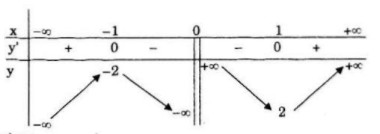
Đồ thị:
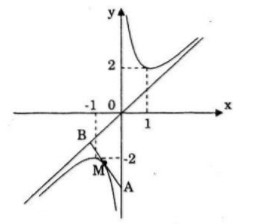
LG b
Tiếp tuyến của đường cong (C) tại điểm M\left( {{x_o};f\left( {{x_o}} \right)} \right) cắt tiệm cận đứng và tiệm cận xiên tại hai điểm A và B. Chứng minh rằng M là trung điểm của đoạn thẳng AB và tam giác OAB có diện tích không phụ thuộc vào vị trí điểm M trên đường cong (C).
Lời giải chi tiết:
Tiệm cận đứng x = 0; Tiệm cận xiên y = x.
Ta có f\left( x \right) = 1 - {1 \over {{x^2}}}.
Phương trình tiếp tuyến của đường cong (C) tại điểm M\left( {{x_o};f\left( {{x_o}} \right)} \right) là y = \left( {1 - {1 \over {x_o^2}}} \right)\left( {x - {x_o}} \right) + {x_o} + {1 \over {{x_o}}}
Thay x = 0 vào phương trình trên, ta được tung độ của điểm A:
{y_A} = \left( {1 - {1 \over {x_o^2}}} \right)\left( { - {x_o}} \right) + {x_o} + {1 \over {{x_o}}} = {2 \over {{x_o}}}.
Vậy A\left( {0;{2 \over {{x_o}}}} \right)
Hoành độ của điểm B là nghiệm của phương trình
\left( {1 - {1 \over {x_o^2}}} \right)\left( {x - {x_o}} \right) + {x_o} + {1 \over {{x_o}}} = x
\Leftrightarrow - {x \over {{x_o}}} + {2 \over {{x_o}}} = 0 \Leftrightarrow x = 2{x_o}
{x_B} = 2{x_o}.
Vậy B\left( {2{x_o};2{x_o}} \right)
Ta có: {x_M} = {x_o} = {{0 + 2{x_o}} \over 2} = {{{x_A} + {x_B}} \over 2}
Vì ba điểm A, M, B thẳng hàng nên từ đó suy ra rằng M là trung điểm của đoạn thẳng AB.
Ta thấy, khoảng cách từ B đến trục Oy bằng 2x0 là độ dài đường cao kẻ từ B của OAB, OA có độ dài bằng 2/x0 .
Diện tích tam giác OAB là
S = {1 \over 2}\left| {{y_A}} \right|\left| {{y_B}} \right| = {1 \over 2}\left| {{2 \over {{x_o}}}} \right|\left| {2{x_o} } \right|=2, với \forall {x_o} \ne 0

