Đề bài
Cho khối hộp \(ABCD.A'B'C'D'\). Chứng minh rằng sáu trung điểm của sáu cạnh \(AB, BC, CC', C'D’, D'A'\) và \(A'A\) nằm trên một mặt phẳng và mặt phẳng đó chia khối hộp thành hai phần có thể tích bằng nhau.
Lời giải chi tiết
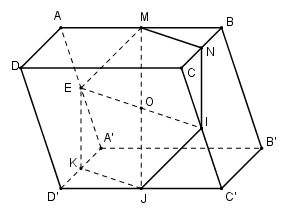
Gọi \(M, N, I, J, K, E\) lần lượt là trung điểm của các cạnh \(AB, BC, CC’, C’D’, D’A’, A’A\) của khối hộp \(ABCD.A’B’C’D’\) tâm \(O\).
Ta có \(O\) là tâm hình bình hành \(ABC’D’\) nên \(M, O, J\) thẳng hàng (\(O\) là trung điểm của \(MJ\)). Mặt khác ba đường thẳng \(MN, EI\) và \(KJ\) đôi một song song với nhau (vì cung song song với \(AC\)) nên chúng đồng phẳng.
Vậy \(6\) điểm \(M, N, I, J, K, E\) cùng nằm trên một mặt phẳng \(\left( \alpha \right)\).
Mp \(\left( \alpha \right)\) chia khối hộp thành hai khối đa diện khối thứ nhất có các đỉnh \(M, N, I, J, K, E, A, C, D, D’\) , khối thứ hai có các đỉnh \(M, N, I, J, K, E, C’, A’, B, B’\).
Phép đối xứng qua điểm \(O\) biến tập hợp đỉnh của khối đa diện thứ nhất thành tập hợp đỉnh của khối đa diện thứ hai. Suy ra hai khối đa diện đó bằng nhau và do đó có thể tích bằng nhau.

