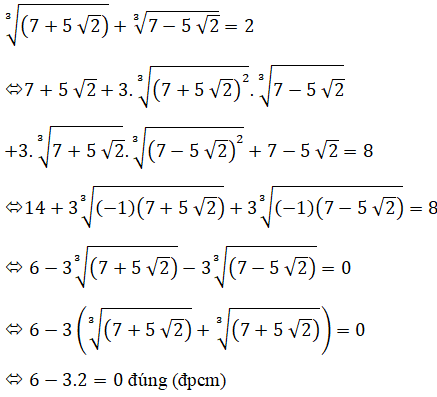Đề bài
Chứng minh 3√7+5√2+3√7−5√2=2
Lời giải chi tiết
Đặt x=3√7+5√2+3√7−5√2
Ta có:
x3=(3√7+5√2+3√7−5√2)3
=7+5√2+7−5√2 +33√(7+5√2)2.3√7−5√2 +33√7+5√2.3√(7−5√2)2
=14+33√(7+5√2)(7−5√2)..(3√7+5√2+3√7−5√2)
=14−3(3√7+5√2+3√7−5√2)
=14−3x.
Từ đó suy ra: x3+3x−14=0(1)
(1)⇔(x−2)(x2+2x+7)=0
⇔x−2=0⇔x=2
(vì x2+2x+7>0)
Vậy 3√7+5√2+3√7−5√2=2
Cách khác: