Cho khối lăng trụ đứng ABC.A′B′C′ có đáy là tam giác ABC vuông tại A,AC=b. ^ACB=600. Đường thẳng BC′ tạo với mp (AA′C′C) một góc 300.
LG a
Tính độ dài đoạn thẳng AC′.
Phương pháp giải:
- Góc giữa đường thẳng và mp bằng góc giữa đt và hình chiếu của nó trên mp.
- Tính AC' dựa và tỉ số lượng giác của góc nhọn trong tam giác vuông.
Lời giải chi tiết:
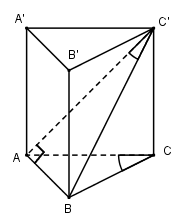
Ta có: BA⊥AC và BA⊥AA′ nên BA⊥(ACC′A′)
Vậy AC′ là hình chiếu của BC′ trên mp (ACC′A′) nên góc giữa BC' và (ACC'A') bằng góc giữa BC' và AC' và bằng ^AC′B=300
Trong tam giác vuông BAC′, ta có: cot300=AC′AB
⇒AC′=AB.cot300
Tam giác ABC vuông tại A có AB=AC.tan600 =b√3
Do đó ⇒AC′=AB.cot300 =b√3.√3=3b
LG b
Tính thể tích khối lăng trụ đã cho.
Phương pháp giải:
Thể tích lăng trụ V=Bh.
Lời giải chi tiết:
Trong tam giác vuông ACC′, ta có: CC′2=AC′2−AC2 =9b2−b2=8b2
⇒CC′=2√2b
Diện tích đáy là: SABC=12AB.AC =12b√3.b=b2√32
Thể tích khối lăng trụ V=S.h =b2√32.2√2b=b3√6

