Dùng phương pháp đổi biến số tính các tích phân sau:
LG a
1∫0√x+1dx;1∫0√x+1dx;
Lời giải chi tiết:
Đặt u=√x+1⇒u2=x+1u=√x+1⇒u2=x+1 ⇒2udu=dx.⇒2udu=dx.
Đổi cận
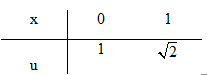
1∫0√x+1dx=√2∫1u.2udu1∫0√x+1dx=√2∫1u.2udu =2√2∫1u2du=2√2∫1u2du =2.u33|√21=23(2√2−1)=2.u33∣∣√21=23(2√2−1)
LG b
π4∫0tanxcos2xdx;π4∫0tanxcos2xdx;
Lời giải chi tiết:
Đặt u=tanx⇒du=dxcos2xu=tanx⇒du=dxcos2x
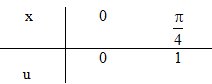
π4∫0tanxcos2xdx=1∫0udu=u22|10=12π4∫0tanxcos2xdx=1∫0udu=u22∣∣10=12
LG c
1∫0t3(1+t4)3dt;
Lời giải chi tiết:
Đặt u=1+t4⇒du=4t3dt ⇒t3dt=du4
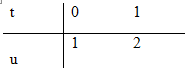
1∫0t3(1+t4)dt =142∫1u3du=14u44|21 =116(16−1)=1516
LG d
1∫05x(x2+4)2dx;
Lời giải chi tiết:
Đặt u=x2+4⇒du=2xdx ⇒xdx=12du
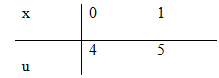
1∫05x(x2+4)2dx=525∫4duu2 =52(−1u)|54 =52(−15+14) =18
LG e
√3∫04x√x2+1dx;
Lời giải chi tiết:
Đặt u=√x2+1⇒u2=x2+1 ⇒udu=xdx
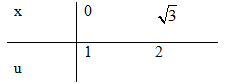
√3∫04x√x2+1dx=42∫1uduu=4u|21=4
LG f
π6∫0(1−cos3x)sin3xdx.
Lời giải chi tiết:
Đặt u=1−cos3x⇒du=3sin3xdx ⇒sin3xdx=13du
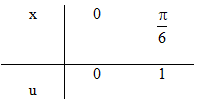
π6∫0(1−cos3x)sin3xdx =131∫0udu=u26|10=16

