Đề bài
Cho hình vuông ABCD nội tiếp đường tròn (O; R). Gọi H là hình gồm các điểm của hình tròn (O; R) nhưng không nằm trong hình vuông. Tính thể tích hình tròn xoay sinh bởi hình H khi quay quanh đường thẳng chứa một đường chéo của hình vuông.
Lời giải chi tiết
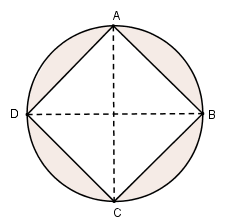
Khi quay quanh đường chéo AC thì:
+ hình tròn (O, R) sinh ra khối cầu (S) có thể tích V(S)=43πR3
+ đoạn thẳng BD sinh ra hình tròn (C)
+ hình vuông ABCD sinh ra hình tròn xoay K gồm hai hình nón có chung đáy là (C) với đỉnh là A và C có thể tích V(K)=2.13πR2.R=23πR3
Do đó H sinh ra khối tròn xoay gồm những điểm thuộc hình cầu (S) nhưng không thuộc K và thể tích V của khối đó là:
V=V(S)−V(K) =43πR3−23πR3=23πR3.

