Đề bài
Hãy chia một khối tứ diện thành hai khối tứ diện sao cho tỉ số thể tích của hai khối tứ diện này bằng một số \(k>0\) cho trước.
Lời giải chi tiết
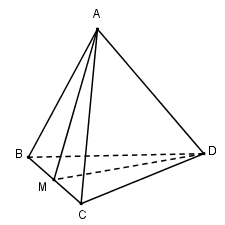
Cho khối tứ diện \(ABCD\).
Trên cạnh \(BC\) lấy một điểm \(M\).
Ta thấy \(d\left( {A,\left( {BMD} \right)} \right) = d\left( {A,\left( {CMD} \right)} \right)\)
Khi đó,
\(\begin{array}{l}
\frac{{{V_{A.BMD}}}}{{{V_{A.CMD}}}} = \frac{{\frac{1}{3}{S_{BMD}}.d\left( {A,\left( {BMD} \right)} \right)}}{{\frac{1}{3}{S_{CMD}}.d\left( {A,\left( {CMD} \right)} \right)}}\\
= \frac{{{S_{BMD}}}}{{{S_{CMD}}}} = \frac{{BM}}{{CM}}
\end{array}\)
Do đó \(\frac{{{V_{A.BMD}}}}{{{V_{A.CMD}}}} = k \Leftrightarrow \frac{{BM}}{{CM}} = k\)
Vậy lấy điểm M sao cho BM=kCM ta được mặt phẳng \((AMD)\) chia khối tứ diện \(ABCD\) thành hai khối tứ diện có tỉ số thể tích bằng \(k\).
Chú ý:
Ngoài cạnh BC thì có thể chọn các cạnh khác của tứ diện để lấy điểm M, chẳng hạn CM=kMD hay AM=kMD ta đều chia được thỏa mãn bài toán.

