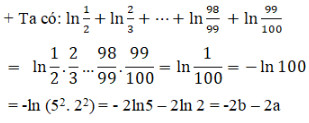Đề bài
Biểu diễn các số sau đây theo a = ln2,b = ln5:
ln500;ln1625;ln6,25
ln12+ln23+...+ln9899+ln99100.
Lời giải chi tiết
+ ln500 = ln(53.22) = ln53+ln22
= 3ln5+2ln2=3b+2a
+ ln(16/25)=ln16-ln25=ln24-ln(52)
=4ln2-2ln5=4a-2b
+ ln6,25=ln(625/100)=ln625-ln100
=ln(54)-ln(52.22)=4ln5 - 2ln5-2ln2
=2ln5-2ln2=2b-2a
ln12+ln23+...+ln9899+ln99100
=ln1−ln2+ln2−ln3+ ...+ln99−ln100
=−ln100=−ln(22.52)
=−2ln2−2ln5=−2a−2b.
Cách khác: