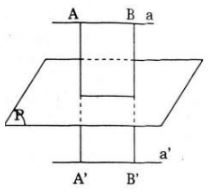
Gọi Đ là phép đối xứng qua mặt phẳng (P) và a là một đường thắng nào đó. Giả sử Đ biến đường thẳng a thành đường thẳng a′. Trong trường hợp nào thì :
LG a
a trùng với a′ ;
Lời giải chi tiết:
a trùng với a′ khi a nằm trên mp(P) hoặc a vuông góc với mp(P).
Thật vậy,
+ Nếu a ⊂ (P), khi đó, lấy điểm A bất kì trên a thì A∈ (P) nên Đ biến A thành A'≡ A.
Vậy Đ biến a thành a’ ≡a
+ Nếu a ⊥ (P). Lấy A bất kì trên a.
Nếu Đ biến A thành A’ thì AA’ ⊥ (P) mà a ⊥ (P), (A) ∈ a ⇒ A' ∈ a ⇒ a' ≡ a
Vậy nếu đường thẳng a nằm trong mp(P) hoặc đường thẳng a vuông góc với mp(P) thì qua Đ biến đường thẳng a thành a’ ≡ a.
LG b
a song song với a′;
Lời giải chi tiết:
a song song với a′ khi a song song với mp(P). Thật vậy,
Nếu a // (P).
Lấy 2 điểm A, B phân biệt trên a giả sử Đ biến A thành A’, B thành B’.
Ta thấy tứ giác ABB’A’ là hình chữ nhật nếu A’B’ // AB hay a’ // a
Vậy để a // a’ thì a// (P).
LG c
a cắt a′;
Lời giải chi tiết:
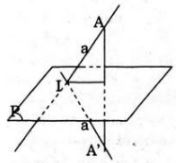
a cắt a′ khi a cắt mp(P) nhưng không vuông góc với mp(P). Thật vậy,
Giả sử a cắt (P) tại I nhưng không vuông góc với (P).
Khi đó, Đ biến I thành chính nó (vì I ∈(P) và biến A ∈a (với A không trùng I) thành A’ sao cho (P) là mặt phẳng trung trực của AA’.
Vậy Đ biến AI thành A’I.
Do a không vuông góc với (P) nên dễ thấy A, I, A’ không thẳng hàng hay AI, A’I cắt nhau tại I tức a, a’ cắt nhau.
Vậy a cắt a’ nếu a cắt (P) nhưng a không vuông góc với (P).
LG d
a và a′ chéo nhau ?
Lời giải chi tiết:
a và a′ không bao giờ chéo nhau.