Xét chiều biến thiên của các hàm số sau:
LG a
y=13x3−2x2+4x−5
Lời giải chi tiết:
TXĐ: D=R
y′=x2−4x+4=(x−2)2≥0, ∀x∈R
Dấu bằng chỉ xảy ra khi x=2
Vậy hàm số đồng biến trên R.
LG b
y=−43x3+6x2−9x−23
Lời giải chi tiết:
TXĐ: D=R
y′=−4x2+12x−9 =−(4x2−12x+9)
=−(2x−3)2≤0,∀x∈R
Dấu bằng chỉ xảy ra khi x=32.
Vậy hàm số nghịch biến trên R.
LG c
y=x2−8x+9x−5
Lời giải chi tiết:
TXĐ: D=R∖{5}
y′=(x2−8x+9)′(x−5)−(x2−8x+9)(x−5)′(x−5)2 =(2x−8)(x−5)−(x2−8x+9)(x−5)2=x2−10x+31(x−5)2
=x2−10x+25+6(x−5)2=(x−5)2+6(x−5)2>0 với mọi x≠5
Vậy hàm số đồng biến trên mỗi khoảng (−∞;5) và (5;+∞).
LG d
y=√2x−x2
Lời giải chi tiết:
Hàm số xác định khi và chỉ khi 2x−x2≥0⇔0≤x≤2.
TXĐ: D=[0;2]
y′=(2x−x2)′2√2x−x2=2−2x2√2x−x2=1−x√2x−x2
y′=0⇔x=1(y=1)
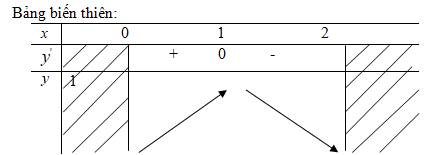
Hàm số đồng biến trên khoảng (0;1) và nghịch biến trên khoảng (1;2).
LG e
y=√x2−2x+3
Lời giải chi tiết:
TXĐ: D=R
(vì x2−2x+3 =(x−1)2+2>0,∀x∈R)
y′=(x2−2x+3)′2√x2−2x+3=2x−22√x2−2x+3 =x−1√x2−2x+3;
y′=0⇔x=1(y=√2)
Bảng biến thiên
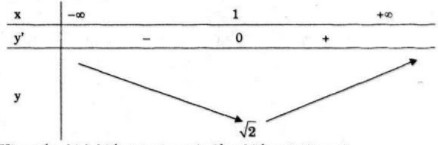
Hàm số nghịch biến trên khoảng (−∞;1) và đồng biến trên khoảng (1;+∞).
LG f
y=1x+1−2x
Lời giải chi tiết:
TXĐ: D=R∖{−1}
y′=−1(x+1)2−2<0,∀x≠−1
Hàm số nghịch biến trên mỗi khoảng (−∞;−1) và (−1;+∞) .

