Tìm giá trị lớn nhất và giá trị nhỏ nhất của các hàm số sau:
LG a
\(y = 2{\sin ^2}x + 2\sin x - 1\)
Lời giải chi tiết:
Đặt \(t = \sin x, - 1 \le t \le 1\)
\(y = f\left( t \right) = 2{t^2} + 2t - 1\)
Ta tìm giá trị lớn nhất và giá trị nhỏ nhất của hàm số \(y = f\left( t \right)\) trên đoạn \(\left[ { - 1;1} \right]\).
Đó cũng là giá trị lớn nhất và giá trị nhỏ nhất của hàm số đã cho trên \(\mathbb R\).
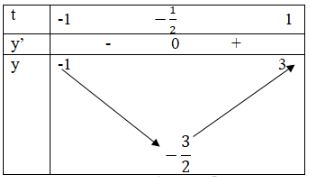
\(f'\left( t \right) = 4t + 2;f'\left( t \right) = 0 \Leftrightarrow t = - {1 \over 2}\)
Ta có: \(f\left( { - 1} \right) = - 1;f\left( { - {1 \over 2}} \right) = - {3 \over 2};\) \(f\left( 1 \right) = 3\)
Bảng biến thiên:
\(\mathop {\min \,\,f\left( t \right)}\limits_{t \in \left[ { - 1;1} \right]} = - {3 \over 2};\,\,\,\,\,\,\mathop {\max \,\,f\left( t \right)}\limits_{t \in \left[ { - 1;1} \right]} = 3\)
Vậy \(\mathop {\min \,\,y}\limits_{x \in {\mathbb{R}}} = - {3 \over 2}\) đạt được khi
\(\sin x = - \frac{1}{2} \Leftrightarrow \left[ \begin{array}{l}
x = - \frac{\pi }{6} + k2\pi \\
x = \frac{{7\pi }}{6} + k2\pi
\end{array} \right.\)
\(\mathop {\max \,\,y}\limits_{x \in {\mathbb{R}}} = 3\) đạt được khi \(\sin x = 1 \Leftrightarrow x = \frac{\pi }{2} + k2\pi \)
LG b
\(y = {\cos ^2}2x - \sin x\cos x + 4\)
Lời giải chi tiết:
Ta có: \(y = 1 - {\sin ^2}2x - {1 \over 2}\sin 2x + 4 \) \(= - {\sin ^2}2x - {1 \over 2}\sin 2x + 5\)
Đặt \(t = \sin 2x, - 1 \le t \le 1\)
\(y = f\left( t \right) = - {t^2} - {1 \over 2}t + 5\)
\(f'\left( t \right) = - 2t - {1 \over 2}\)
\(f'\left( t \right) = 0 \Leftrightarrow t = - {1 \over 4} \in \left[ { - 1;1} \right]\)
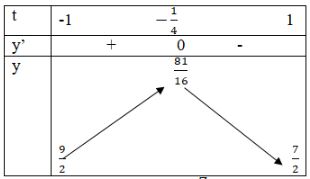
Ta có: \(f\left( { - 1} \right) = {9 \over 2};f\left( { - {1 \over 4}} \right) = {{81} \over {16}};\) \(f\left( 1 \right) = {7 \over 2}\)
BBT:
\(\mathop {\min \,\,f\left( t \right)}\limits_{t \in \left[ { - 1;1} \right]} = {7 \over 2};\mathop {\max \,\,f\left( t \right)}\limits_{t \in \left[ { - 1;1} \right]} = {{81} \over {16}}\)
Vậy \(\mathop {\min \,\,y}\limits_{x \in {\mathbb{R}}} = {7 \over 2}\) đạt được khi \(\sin 2x = 1 \Leftrightarrow 2x = \frac{\pi }{2} + k2\pi \) \( \Leftrightarrow x = \frac{\pi }{4} + k\pi \)
\(\mathop {\max \,\,y}\limits_{x \in {\mathbb{R}}} = {{81} \over {16}}\) đạt được khi
\(\sin 2x = - \frac{1}{4} \) \(\Leftrightarrow \left[ \begin{array}{l}
2x = \arcsin \left( { - \frac{1}{4}} \right) + k2\pi \\
2x = \pi - \arcsin \left( { - \frac{1}{4}} \right) + k2\pi
\end{array} \right.\) \( \Leftrightarrow \left[ \begin{array}{l}
x = \frac{1}{2}\arcsin \left( { - \frac{1}{4}} \right) + k\pi \\
x = \frac{\pi }{2} - \frac{1}{2}\arcsin \left( { - \frac{1}{4}} \right) + k\pi
\end{array} \right.\)