LG a
Khảo sát sự biến thiên và vẽ đồ thị của hàm số: y=2x−1x+1
Lời giải chi tiết:
Tập xác định: D=R∖{−1}
y′=3(x+1)2>0∀x∈D
Hàm số đồng biến trên khoảng (−∞;−1) và (−1;+∞)
Hàm số không có cực trị
Giới hạn
lim
Tiệm cận đứng y=2
\eqalign{ & \mathop {\lim }\limits_{x \to {1^ - }} y = + \infty \cr & \mathop {\lim }\limits_{x \to {1^ + }} y = - \infty \cr}
Tiệm cận đứng: x=-1
Bảng biến thiên:
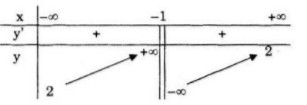
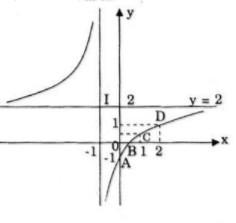
Đồ thị giao Ox tại điểm \left( {{1 \over 2};0} \right)
Đồ thị giao Oy tại điểm (0;-1)
Đồ thị hàm số nhận điểm I(-1;2) làm tâm đối xứng.
LG b
Với các giá trị nào của m, đường thẳng \left( {{d_m}} \right) đi qua điểm A(-2;2) và có hệ số góc m cắt đồ thị của hàm số đã cho:
• Tại hai điểm phân biệt?
• Tại hai điểm thuộc hai nhánh của đồ thị?
Lời giải chi tiết:
Phương trình đường thẳng \left( {{d_m}} \right) qua điểm A(-2;2) có hệ số góc m là:
y - 2 = m\left( {x + 2} \right) hay y = mx + 2m + 2
Hoành độ giao điểm của đường thẳng \left( {{d_m}} \right) và đường cong đã cho là nghiệm phương trình:
\eqalign{ & mx + 2m + 2 = {{2x - 1} \over {x + 1}} \cr & \Rightarrow \left( {mx + 2m + 2} \right)\left( {x + 1} \right) = 2x - 1\,\,\,\,\,\left( 1 \right) \cr & \Leftrightarrow m{x^2} + 3mx + 2m + 3 = 0\,\,\,\left( 2 \right) \cr}
• Đường thẳng \left( {{d_m}} \right) cắt đường cong tại hai điểm phân biệt khi và chỉ khi phương trình (2) có hai nghiệm phân biệt khác -1, tức là
\begin{array}{l} \left\{ \begin{array}{l} a \ne 0\\ \Delta > 0\\ f\left( { - 1} \right) \ne 0 \end{array} \right.\\ \Leftrightarrow \left\{ \begin{array}{l} m \ne 0\\ 9{m^2} - 4m\left( {2m + 3} \right) > 0\\ m.{\left( { - 1} \right)^2} + 3m.\left( { - 1} \right) + 2m + 3 \ne 0 \end{array} \right.\\ \Leftrightarrow \left\{ \begin{array}{l} m \ne 0\\ {m^2} - 12m > 0\\ 3 \ne 0\left( {\text{đúng}} \right) \end{array} \right. \Leftrightarrow \left\{ \begin{array}{l} m \ne 0\\ \left[ \begin{array}{l} m > 12\\ m < 0 \end{array} \right. \end{array} \right.\\ \Leftrightarrow \left[ \begin{array}{l} m > 12\\ m < 0 \end{array} \right.(*) \end{array}
• Hai nhánh của đường cong nằm về hai phía của đường tiệm cận đứng x = -1 của đồ thị.
\Leftrightarrow Đường thẳng \left( {{d_m}} \right) cắt đường cong tại hai điểm thuộc hai nhánh của nó
\Leftrightarrow (1) có hai nghiệm {x_1},\,{x_2} thỏa mãn {x_1} < - 1 < {x_2}
\eqalign{ & \Leftrightarrow {x_1} + 1 < 0 < {x_2} + 1\cr&\Leftrightarrow \left( {{x_1} + 1} \right)\left( {{x_2} + 1} \right) < 0 \cr & \Leftrightarrow {x_1}.{x_2} + {x_1} + {x_2} + 1 < 0 \cr&\Leftrightarrow {{2m + 3} \over m} - {{3m} \over m} + 1 < 0 (\text{ Vi-et })\cr & \Leftrightarrow {3 \over m} < 0 \cr}
Kết hợp với (*) được m < 0
Vậy với m < 0 thì \left( {{d_m}} \right) cắt (C) tại hai điểm phân biệt thuộc hai nhánh của đồ thị.
Cách khác:
\Leftrightarrow (1) có hai nghiệm {x_1},\,{x_2} thỏa mãn {x_1} < - 1 < {x_2}
⇔ af(-1)<0
⇔ m(m(-1)2+3m(-1)+2m+3)<0
⇔ 3m<0 ⇔ m < 0
Vậy với m ∈(-∞;0) thì đường thẳng (dm) sẽ cắt đồ thị (C) tại 2 điểm phân biệt ∈ 2 nhánh đồ thị.

