Đề bài
Cho tam giác \(ABC\) vuông tại \(A\), \(AB = c,\,AC = b\) . Gọi \({V_1},{V_2},{V_3}\) là thể tích các khối tròn xoay sinh bởi tam giác đó (kê cả các điểm trong) khi lần lượt quay quanh \(AB, AC, BC\).
a) Tính \({V_1},{V_2},{V_3}\) theo \(b, c\).
b) Chứng minh rằng \({1 \over {V_3^2}} = {1 \over {V_1^2}} + {1 \over {V_2^2}}\)
Lời giải chi tiết
a) Khi quay tam giác \(ABC\) quanh \(AB\) ta được khối nón có chiều cao \(AB = c\) và bán kính đáy \(AC = b\) nên có thể tích \(V_1 = {1 \over 3}\pi c{b^2}\)
Tương tự khi quay tam giác \(ABC\) quanh \(AC\) ta được khối nón có thể tích \({V_2} = {1 \over 3}\pi b{c^2}\)
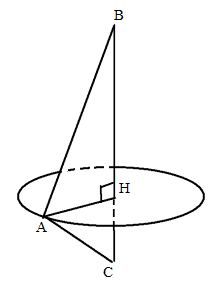
Gọi \(AH\) là chiều cao của tam giác \(ABC\). Khi quay tam giác \(ABC\) quanh \(BC\) ta được hai khối nón sinh bởi hai tam giác \(ABH\) và \(ACH\).
Ta có: \(\frac{1}{{A{H^2}}} = \frac{1}{{A{B^2}}} + \frac{1}{{A{C^2}}} = \frac{{A{C^2} + A{B^2}}}{{A{B^2}.A{C^2}}} \)
\(\Rightarrow A{H^2} = \frac{{A{B^2}.A{C^2}}}{{A{B^2} + A{C^2}}} = \frac{{{b^2}{c^2}}}{{{b^2} + {c^2}}} \) \( \Rightarrow AH = \frac{{bc}}{{\sqrt {{b^2} + {c^2}} }}\)
Khi đó ta có
\({V_3} = {1 \over 3}\pi A{H^2}.BH + {1 \over 3}\pi A{H^2}.CH \) \(= {1 \over 3}\pi AH^2.BC \) \(= {1 \over 3}\pi {\left( {{{bc} \over {\sqrt {{b^2} + {c^2}} }}} \right)^2}\sqrt {{b^2} + {c^2}} \) \(= {1 \over 3}{{\pi {b^2}{c^2}} \over {\sqrt {{b^2} + {c^2}} }}\)
b) Ta có: \({1 \over {V_3^2}} = {{9\left( {{b^2} + {c^2}} \right)} \over {\pi ^2 {b^4}{c^4}}}\)
\({1 \over {V_1^2}} + {1 \over {V_2^2}} = {9 \over {\pi ^2{c^2}{b^4}}} + {9 \over {\pi ^2{b^2}{c^4}}} \) \(= {{9\left( {{b^2} + {c^2}} \right)} \over {\pi^2 {b^4}{c^4}}} = {1 \over {V_3^2}}\)
