LG a
Tìm tiệm cận đứng và tiệm cận xiên của đồ thị (C) của hàm số:
y=x2−2x+2x−3
Lời giải chi tiết:
Ta có: y=x2−2x+2x−3=x+1+5x−3
TXĐ: D=R∖{3}
Vì lim và \mathop {\lim }\limits_{x \to {3^ - }} y = - \infty nên x = 3 là tiệm cận đứng.
\mathop {\lim }\limits_{x \to \pm \infty } \left[ {y - \left( {x + 1} \right)} \right] = \mathop {\lim }\limits_{x \to \pm \infty } {5 \over {x - 3}} = 0 nên y = x + 1 là tiệm cận xiên.
Chú ý:
Ta thực hiện chia tử cho mẫu theo lược đồ sau:
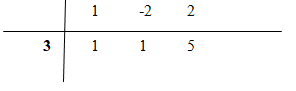
Ở đó, 1, -2, 2 là các hệ số của tử và 3 là nghiệm cuả mẫu.
Cách thực hiện:
+ Viết 1 -2 2 ở dòng trên, viết 3 ở cột trước đó, hạ 1 thẳng số 1 đầu tiên.
+ Lấy 1 nhân 3 cộng (-2) được 1, viết 1 thẳng -2.
+ Lấy 1 nhân 3 cộng 2 bằng 5, viết 5.
Từ đó viết được y = \frac{{{x^2} - 2x + 2}}{{x - 3}} = x + 1 + \frac{5}{{x - 3}}.
Hoặc các em cũng có thể thực hiện chia đa thức tử cho mẫu cũng được kết quả như vậy.
LG b
Xác định giao điểm I của hai tiệm cận trên và viết công thức chuyển hệ tọa độ trong phép tịnh tiến theo véc tơ \overrightarrow {OI} .
Lời giải chi tiết:
Tọa độ giao điểm I(x;y) của hai tiệm cận là nghiệm của hệ phương trình
\left\{ \matrix{ x = 3 \hfill \cr y = x + 1 \hfill \cr} \right. \Leftrightarrow \left\{ \matrix{ x = 3 \hfill \cr y = 4 \hfill \cr} \right.
Vậy I(3;4) là giao điểm của hai tiệm cận trên.
Công thức chuyển hệ tọa độ trong phép tịnh tiến theo véc tơ \overrightarrow {OI} là
\left\{ \matrix{ x = X + 3 \hfill \cr y = Y + 4 \hfill \cr} \right.
LG c
Viết phương trình của đường cong (C) đối với hệ tọa độ IXY.
Từ đó suy ra rằng I là tâm đối xứng của đường cong (C).
Lời giải chi tiết:
Phương trình của đường cong (C) đối với hệ tọa độ IXY là
Y + 4 = X + 3 + 1 + {5 \over {X + 3 - 3}} \Leftrightarrow Y = X + {5 \over X}
Đây là hàm số lẻ, do đó (C) nhận gốc tọa độ I làm tâm đối xứng.

