LG a
Khảo sát sự biến thiên và vẽ đồ thị của hàm số y=x−2x−1
Lời giải chi tiết:
Tập xác định: D=R∖{1}
y′=1+2(x−1)2>0,∀x∈D
Vậy hàm số đồng biến trên khoảng (−∞;1) và (1;+∞)
limx→1−y=+∞limx→1+y=−∞
Do đó x=1 là tiệm cận đứng.
limx→±∞(y−x)=limx→±∞(−2x−1)=0
Vậy y=x là tiệm cận xiên.
Bảng biến thiên:
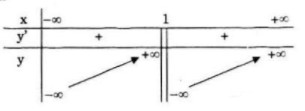
Đồ thị giao Ox tại (−1;0),(2;0)
Đồ thị giao Oy tại (0;2)
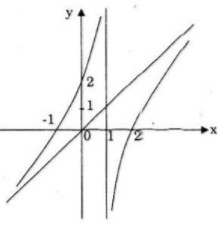
LG b
Viết phương trình tiếp tuyến của đồ thị hàm số đã cho biết rằng tiếp tuyến đó đi qua điểm (3;3).
Lời giải chi tiết:
Ta có: y′=1+2(x−1)2
Phương trình tiếp tuyến với đồ thị hàm số đã cho tại điểm M(xo;xo−2xo−1)∈(C) là:
(d):y−xo+2xo−1 =[1+2(xo−1)2](x−xo)(xo≠1)
Vì (3;3)∈d nên 3−xo+2xo−1=(xo−1)2+2(xo−1)2(3−xo)
⇔(3−xo)(xo−1)2+2(xo−1)=(x2o−2xo+3)(3−xo)
\begin{array}{l} \Leftrightarrow \left( {3 - {x_o}} \right)\left( {x_o^2 - 2{x_o} + 1} \right) + 2{x_o} - 2\\ = 3x_o^2 - 6{x_o} + 9 - x_o^3 + 2x_o^2 - 3{x_o}\\ \Leftrightarrow 3x_o^2 - x_o^3 - 6{x_o} + 2x_o^2 + 3 - {x_o} + 2{x_o} - 2\\ = 3x_o^2 - 6{x_o} + 9 - x_o^3 + 2x_o^2 - 3{x_o}\\ \Leftrightarrow 4{x_o} - 8 = 0\\ \Leftrightarrow {x_o} = 2\\ \Rightarrow {y_o} = 2 - \frac{2}{{2 - 1}} = 0 \end{array}
\Rightarrow M\left( {2;0} \right)
Vậy phương trình tiếp tuyến cần tìm là: y = 3\left( {x - 2} \right) hay y = 3x - 6.
Cách khác:
Gọi phương trình đường thẳng (d) có hệ số góc k đi qua A(3; 3) có dạng
y-3=k(x-3) <=> y=k(x-3)+3
(d) là tiếp tuyến của đồ thị hàm số khi và chỉ khi hệ phương trình sau có nghiệm

Thế (2) vào (1) ta được:
\begin{array}{l} \frac{{{x^2} - x - 2}}{{x - 1}} = \left( {1 + \frac{2}{{{{\left( {x - 1} \right)}^2}}}} \right)\left( {x - 3} \right) + 3\\ \Leftrightarrow \frac{{{x^2} - x - 2}}{{x - 1}} = \frac{{{{\left( {x - 1} \right)}^2} + 2}}{{{{\left( {x - 1} \right)}^2}}}\left( {x - 3} \right) + 3\\ \Leftrightarrow \frac{{{x^2} - x - 2}}{{x - 1}} = \frac{{\left( {{x^2} - 2x + 3} \right)\left( {x - 3} \right)}}{{{{\left( {x - 1} \right)}^2}}} + 3\\ \Leftrightarrow \frac{{\left( {{x^2} - x - 2} \right)\left( {x - 1} \right)}}{{{{\left( {x - 1} \right)}^2}}}\\ = \frac{{\left( {{x^2} - 2x + 3} \right)\left( {x - 3} \right)}}{{{{\left( {x - 1} \right)}^2}}} + \frac{{3{{\left( {x - 1} \right)}^2}}}{{{{\left( {x - 1} \right)}^2}}}\\ \Rightarrow \left( {{x^2} - x - 2} \right)\left( {x - 1} \right)\\ = \left( {{x^2} - 2x + 3} \right)\left( {x - 3} \right) + 3\left( {{x^2} - 2x + 1} \right)\\ \Leftrightarrow {x^3} - {x^2} - 2x - {x^2} + x + 2\\ = {x^3} - 2{x^2} + 3x - 3{x^2} + 6x - 9 + 3{x^2} - 6x + 3\\ \Leftrightarrow - 4x + 8 = 0\\ \Leftrightarrow x = 2 \end{array}
* Với x = 2 thay vào (2) ta được k = 3.
Vậy phương trình tiếp tuyến là
y = 3(x- 3) + 3 hay y = 3x – 6

