Bài 57 Trang 177 SGK Đại số và Giải tích 12 Nâng cao

130 lượt xem

Lựa chọn câu để xem lời giải nhanh hơn

LG a
LG b

Cho hình phẳng A được giới hạn bởi đường cong có phương trình $x - {y^2} = 0$ và các đường thẳng $y = 2,x = 0$ . Tính thể tích khối tròn xoay tạo thành khi quay A.

LG a

Quanh trục hoành;

Phương pháp giải:

Sử dụng công thức tính thể tích $V = \int\limits_a^b {[{f^2}\left( x \right)-g^2(x)]dx}$

Lời giải chi tiết:

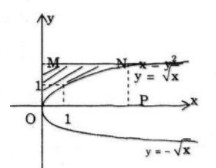
Ta có: $x - {y^2} = 0 \Leftrightarrow y = \pm \sqrt x$

Hoành độ giao điểm của đường cong $y=\sqrt x$ và $y=2$ là:

$\sqrt x=2\Rightarrow x=4$

Thể tích khối tròn xoay tạo thành khi quay A quanh $Ox$ là:

$V = \pi \int\limits_0^4 {\left( {2^2} - (\sqrt x)^2 \right)} dx$ $= \pi \int\limits_0^4 {\left( {4 - x} \right)dx}$ $= \left. {\pi \left( {4x - {{{x^2}} \over 2}} \right)} \right|_0^4 = 8\pi$

LG b

Quanh trục tung

Phương pháp giải:

Sử dụng công thức tính thể tích $V = \int\limits_a^b {{f^2}\left( y \right)dy}$

Lời giải chi tiết:

Thể tích khối tròn xoay tạo thành khi quay A quanh $Oy$ là:

$V = \pi \int\limits_0^2 {{{\left( {{y^2}} \right)}^2}dy} = \pi \int\limits_0^2 {{y^4}dy}$ $= \left. {{\pi \over 5}{y^5}} \right|_0^2 = {{32\pi } \over 5}$

SGK Toán 12 Nâng cao