Đề bài
Hai đỉnh của một khối tám mặt đều được gọi là hai đỉnh đối diện nếu chúng không cùng thuộc một cạnh của khối đó. Đoạn thẳng nối hai đỉnh đối diện gọi là đường chéo của khối tám mặt đều. Chứng minh rằng trong khối tám mặt đều:
a) Ba đường chéo cắt nhau tại trung điểm của mỗi đường ;
b) Ba đường chéo đôi một vuông góc với nhau ;
c) Ba đường chéo bằng nhau.
Lời giải chi tiết
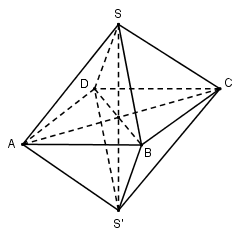
a) Giả sử SABCDS′ là khối tám mặt đều. Ba đường chéo của nó là SS′,AC và BD.
Bốn điểm A,B,C,D cách đều hai điểm S và S′ nên cùng nằm trên một mặt phẳng trung trực của SS'.
Mà AB=BC=CD=DA nên ABCD là hình thoi.
Do đó AC, BD cắt nhau tại trung điểm O của mỗi đường.
Tương tự ta cũng có ASCS' là hình thoi nên đường chéo AC, SS' cắt nhau tại trung điểm O của mỗi đường.
Vậy AC, BD, SS' cắt nhau tại trung điểm O của mỗi đường.
b) Từ câu a, ABCD là hình thoi nên AC ⊥ BD.
Tương tự AC⊥SS′ và BD⊥SS′.
Do đó AC, BD, SS' đôi một vuông góc với nhau.
c) Cách 1. Dễ thấy ΔABD = ΔSBD (c-c-c) nên các trung tuyến tương ứng bằng nhau tức là AO = SO
=> AC = SS', tương tự, AC = BD.
Vậy AC = BD = SS' (đpcm).
Cách 2. Vì SO ⊥ (ABCD) nên AO, OB là hình chiếu của SA, SB trên (ABCD)
Mà SA = SB ⇒ OA = OB ⇒ AC = DB.
Tương tự, AC = SS'.
Vậy AC = BD = SS'.

