Câu 1. Cho hình hộp ABCD.A’B’C’D’. Gọi N là điểm nằm trên cạnh AB và \(\left( \alpha \right)\) là mặt phẳng đi qua ba điểm D, N, B’.
LG a
Mặt phẳng \(\left( \alpha \right)\) cắt hình hộp đã cho theo thiết diện là hình gì?
Lời giải chi tiết:
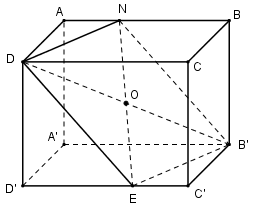
Giả sử \(\left( \alpha \right) \cap C'D' = E\) thì thiết diện của hình hộp khi cắt bởi \(mp\left( \alpha \right)\) là tứ giác DNB’E.
Ta có:
\(\left\{ \matrix{
\left( \alpha \right) \cap \left( {ABCD} \right) = DN \hfill \cr
\left( \alpha \right) \cap \left( {A'B'C'D'} \right) = B'E \hfill \cr
\left( {ABCD} \right)\parallel \left( {A'B'C'D'} \right) \hfill \cr} \right. \Rightarrow DN\parallel B'E.\)
Tương tự ta có:
\(\left\{ \matrix{
\left( \alpha \right) \cap \left( {AA'B'B} \right) = {NB'} \hfill \cr
\left( \alpha \right) \cap \left( {CC'D'D} \right) = DE \hfill \cr
\left( {AA'B'B} \right)\parallel \left( {CC'D'D} \right) \hfill \cr} \right. \Rightarrow NB'\parallel DE.\)
Xét tứ giác DNB’E có: DN // B’E, NB’ // DE.
Vậy DNB’E là hình bình hành.
LG b
Chứng minh rằng mặt phẳng \(\left( \alpha \right)\) phân chia khối hộp đã cho thành hai khối đa diện \({H_1}\) và \({H_2}\) bằng nhau.
Lời giải chi tiết:
\(mp\left( \alpha \right)\) chia khối hộp thành hai khối đa diện \({H_1}:ADNA'B'ED'\) và \({H_2}:C'B'ECDNB.\)
Gọi O là giao điểm hai đường chéo B’D và NE của hình bình hành DNB’E suy ra O là trung điểm của B’D. Do đó O là tâm hình hộp ABCD.A’B’C’D’.
Gọi \({D_{(O)}}\) là phép đối xứng qua tâm O ta có:
\({D_{(O)}}\): \(A \to C'\)
\(\eqalign{
& N \to E \cr
& B' \to D \cr
& E \to N \cr
& D' \to B \cr
& A' \to C \cr
& D \to B' \cr} \)
\( \Rightarrow \)\({D_{(O)}}\): \(ADNA'B'ED' \to C'B'ECDNB\) hay \({D_{(O)}}\): \({H_1} \to {H_2}.\)
Mà phép đối xứng tâm O là phép dời hình nên \({V_{{H_1}}} = {V_{{H_2}}}.\)
LG c
Tính tỉ số thể tích của khối đa diện \({H_1}\) và thể tích của khối tứ diện AA’BD.
Lời giải chi tiết:
Gọi \({V_{ABCD.A'B'C'D'}} = V.\)
Ta có: \({V_{AA'BD}} = {V_{A'.ABD}}.\)
\({S_{\Delta ABD}} = {1 \over 2}{S_{ABCD}} \)
\(\Rightarrow {V_{A'.ABD}} = {1 \over 3}AA'.{S_{\Delta ABD}} \)\(= {1 \over 3}.AA'.{1 \over 2}{S_{ABCD}} = {1 \over 6}{V_{ABCD.A'B'C'D'}} = {V \over 6}.\)
Mà \({V_{{H_1}}} = {V_{{H_2}}} = {V \over 2}.\)
Suy ra \({{{V_{{H_1}}}} \over {{V_{AA'BD}}}} = {{{V \over 2}} \over {{V \over 6}}} = 3.\)

