Khảo sát sự biến thiên và vẽ đồ thị của các hàm số sau:
LG a
\(y = {{{x^2} - 3x + 6} \over {x - 1}}\)
Lời giải chi tiết:
\(y = x- 2 + {4 \over {x - 1}}\)
TXĐ: \(D =\mathbb R\backslash \left\{ 1 \right\}\)
\(\mathop {\lim }\limits_{x \to {1^ + }} y = + \infty ;\,\mathop {\lim }\limits_{x \to {1^ - }} y = - \infty \) nên \(x = 1\) là tiệm cận đứng.
\(\mathop {\lim }\limits_{x \to \pm \infty } \left[ {y - \left( {x - 2} \right)} \right] = \mathop {\lim }\limits_{x \to \pm \infty } {4 \over {x - 1}} = 0\) nên \(y = x – 2\) là tiệm cận xiên.
\(\eqalign{
& y' = 1 - {4 \over {{{\left( {x - 1} \right)}^2}}} \cr&= {{{{\left( {x - 1} \right)}^2} - 4} \over {{{\left( {x - 1} \right)}^2}}} = {{\left( {x - 3} \right)\left( {x + 1} \right)} \over {{{\left( {x - 1} \right)}^2}}} \cr
& y' = 0 \Leftrightarrow \left[ \matrix{
x = - 1;\,\,\,y\left( { - 1} \right) = -5 \hfill \cr
x = 3;\,\,\,y\left( 3 \right) = 3 \hfill \cr} \right. \cr} \)
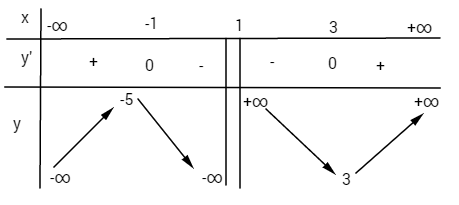
Hàm số đồng biến trên khoảng (-∞; -1) và (3; +∞)
Hàm số nghịch biến trên khoảng (-1;1) và (1;3)
yCĐ=y(-1)=-5;yCT=y(3)=3
Đồ thị:
+) Đồ thị giao với Oy (0; -6)
+) Đồ thị đi qua A(-3; -6)
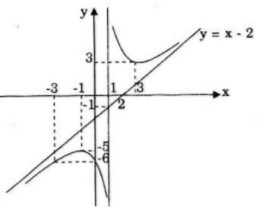
Đồ thị nhận giao điểm \(I(1;-1)\) của hai đường tiệm cận làm tâm đối xứng.
LG b
\(y = {{2{x^2} - x + 1} \over {1 - x}}\)
Lời giải chi tiết:
\(y = {{ - 2{x^2} + x - 1} \over {x - 1}}\)
\(y = - 2x - 1 - {2 \over {x - 1}}\)
TXĐ: \(D =\mathbb R\backslash \left\{ 1 \right\}\)
Vì \(\mathop {\lim }\limits_{x \to {1^ - }} y = + \infty ;\mathop {\lim }\limits_{x \to {1^ + }} y = - \infty \) nên tiệm cận đứng: \(x = 1\)
Vì \(\mathop {\lim }\limits_{x \to \pm \infty } \left[ {y - \left( { - 2x - 1} \right)} \right] \) \(= \mathop {\lim }\limits_{x \to \pm \infty } \left( { - \frac{2}{{x - 1}}} \right) = 0\) nên tiệm cận xiên: \(y = -2x – 1\)
\(\eqalign{
& y' = - 2 + {2 \over {{{\left( {x - 1} \right)}^2}}}\cr& = {{ - 2{{\left( {x - 1} \right)}^2} + 2} \over {{{\left( {x - 1} \right)}^2}}} = {{ - 2{x^2} + 4x} \over {{{\left( {x - 1} \right)}^2}}} \cr
& y' = 0 \Leftrightarrow \left[ \matrix{
x = 0;\,\,\,\,\,y\left( 0 \right) = 1 \hfill \cr
x = 2;\,\,\,\,\,\,y\left( 2 \right) = - 7 \hfill \cr} \right. \cr} \)
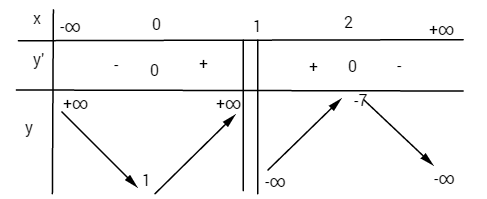
Hàm số đồng biến trên khoảng (0;1)và (1;2)
Hàm số nghịch biến trên khoảng (-∞, 0) và (2; +∞)
yCĐ = y(2) = -7; yCT = y(0) = 1
Điểm đặc biệt:
\(x = 0 \Rightarrow y = 1\)
\(x = -1 \Rightarrow y = 2\)
Đồ thị:
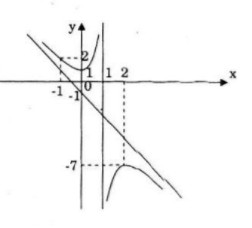
Đồ thị nhận \(I(1;-3)\) làm tâm đối xứng.
LG c
\(y = {{2{x^2} + 3x - 3} \over {x + 2}}\)
Lời giải chi tiết:
\(y = 2x - 1 - {1 \over {x + 2}}\)
• TXĐ: \(D =\mathbb R\backslash \left\{ { - 2} \right\}\)
• Tiệm cận đứng: \(x = 2\) vì \(\mathop {\lim }\limits_{x \to - {2^ - }} y = + \infty ;\mathop {\lim }\limits_{x \to - {2^ + }} y = - \infty \)
Tiệm cận xiên: \(y = 2x -1\) vì \(\mathop {\lim }\limits_{x \to \pm \infty } \left[ {y - \left( {2x - 1} \right)} \right] \) \(= \mathop {\lim }\limits_{x \to \pm \infty } \left( { - \frac{1}{{x + 2}}} \right) = 0\)
• \(y' = 2 + {1 \over {{{\left( {x + 2} \right)}^2}}} > 0\) với mọi \(x \ne - 2\) nên hàm số đồng biến trên các khoảng (-∞; -2) và (-2; +∞)
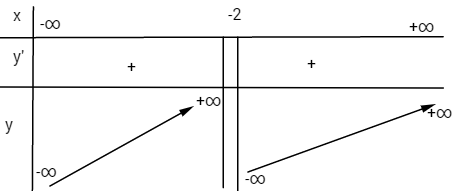
• Điểm đặc biệt: \(x = 0 \Rightarrow y = - {3 \over 2}\)
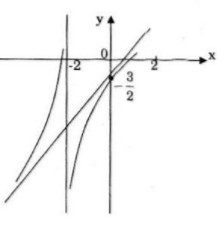
Đồ thị nhận \(I(-2; -5)\) làm tâm đối xứng.
LG d
\(y = - x + 2 + {1 \over {x - 1}}\)
Lời giải chi tiết:
\(y = - x + 2 + {1 \over {x - 1}}\)
• TXĐ: \(D =\mathbb R\backslash \left\{ 1 \right\}\)
• Tiệm cận đứng: \(x = 1\) vì \(\mathop {\lim }\limits_{x \to {1^ - }} y = - \infty ;\mathop {\lim }\limits_{x \to {1^ + }} y = + \infty \)
Tiệm cận xiên \(y = -x +2\) vì \(\mathop {\lim }\limits_{x \to \pm \infty } \left[ {y - \left( { - x + 2} \right)} \right] = \mathop {\lim }\limits_{x \to \pm \infty } \left( {\frac{1}{{x - 1}}} \right) = 0\)
• \(y' = - 1 - {1 \over {{{\left( {x - 1} \right)}^2}}} < 0\) với mọi \(x \ne 1\) nên hàm số luôn nghịch biến trên (-∞;1) và 1; +∞)
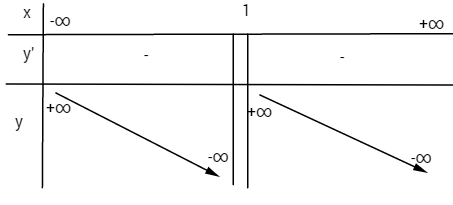
• Điểm đặc biệt: \(x = 0 \Rightarrow y = 1\)
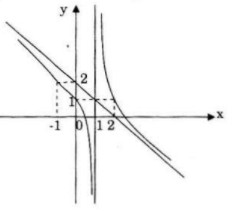
Đồ thị nhận điểm \(I(1;-1)\) làm tâm đối xứng.

