Đề bài
Độ giảm huyết áp của một bệnh nhân được cho bởi công thức: \(G\left( x \right) = 0,025{x^2}\left( {30 - x} \right)\), trong đó \(x\) là liều lượng thuốc được tiêm cho bệnh nhân ( \(x\) được tính bằng miligam). Tính liều lượng thuốc cần tiêm cho bệnh nhân để huyết áp giảm nhiều nhất và tính độ giảm đó.
Lời giải chi tiết
\(D = \left( {0; + \infty } \right)\)
\(G\left( x \right) = 0,75{x^2} - 0,025{x^3}\)
\(G'\left( x \right) = 1,5x - 0,075{x^2}\)
\(G'\left( x \right) = 0 \Leftrightarrow x = 0\) hoặc \(x = 20\).
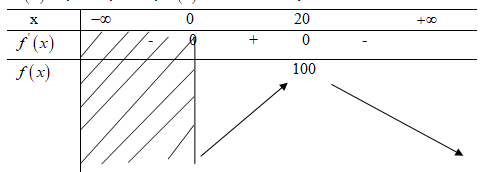
\(\eqalign{
& \mathop {\max G\left( x \right)}\limits_{x > 0} = G\left( {20} \right) = 100 \cr } \)
Vậy liều lượng thuốc cần tiêm cho bệnh nhân để huyết áp giảm nhiều nhất là \(20\) mg.
Khi đó, độ giảm huyết áp là \(100\).

