Đề bài
Cho hình lục giác đều ABCDEF cạnh a.
a) Tính thể tích hình tròn xoay sinh bởi lục giác đó khi quay quanh đường thẳng AD.
b) Tính thế tích hình tròn xoay sinh bởi lục giác đó khi quay quanh đường thẳng đi qua trung điểm của các cạnh AB và DE.
Lời giải chi tiết
a)
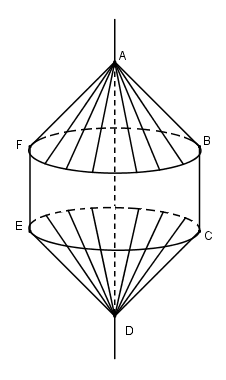
Khi quay lục giác dều ABCDEF quanh đường thẳng AD, ta được khối tròn xoay hợp bởi ba khối:
+ Khối nón \({N_1}\) sinh bởi tam giác ABF
+ Khối trụ T sinh bởi hình chữ nhật BCEF
+ Khối nón \({N_2}\) sinh bởi tam giác DCE.
Hai khối nón và trụ đều có bán kính đáy là \(R = {{BF} \over 2} = {{a\sqrt 3 } \over 2}.\)
Khối trụ có chiều cao a và các khối nón có chiều cao \({a \over 2}.\)
Vậy khối tròn xoay sinh bởi lục giác đã cho có thể tích là:
\(V = \pi {\left( {{{a\sqrt 3 } \over 2}} \right)^2}a + 2.{1 \over 3}\pi {\left( {{{a\sqrt 3 } \over 2}} \right)^2}.{a \over 2} \) \(= \pi {a^3}.\)
b)
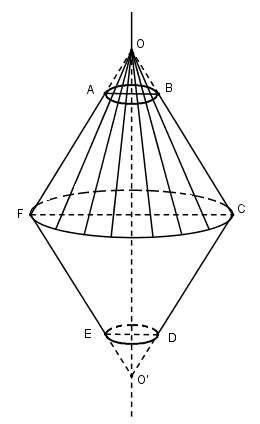
Gọi \(\Delta \) là đường thẳng nối trung điểm của AB và ED.
Khi đó BC và AF cắt nhau tại điểm O trên \(\Delta \), CD và FE cắt nhau tại O’ trên \(\Delta \).
Gọi V, \({V_1},{V_2}\) là thể tích các khối tròn xoay lần lượt sinh ra bởi lục giác đều ABCDEF, tam giác OCF và tam giác OAB khi quay quanh \(\Delta \), ta có:
\(\eqalign{
& {V_1} = {1 \over 3}\pi {a^2}a\sqrt 3 = {{\pi {a^3}\sqrt 3 } \over 3} \cr
& {V_2} = {1 \over 3}\pi {\left( {{a \over 2}} \right)^2}{{a\sqrt 3 } \over 2} \cr &= {{\pi {a^3}\sqrt 3 } \over {24}}. \cr} \)
Do đó \(V = 2\left( {{V_1} - {V_2}} \right) = {{7\sqrt 3 \pi {a^3}} \over {12}}.\)
